Structural design with Alloy

In this chapter we will explain how Alloy can be used to explore the design of a file system. The goal of the chapter is to introduce the key concepts of Alloy, namely the concept of signature field which was not introduced in the previous chapter, so our example will be purposely simple, a very high-level abstraction of a real file system. We will focus only on the structural aspects of the design, namely our main goal is to describe how files and directories are organised (the specification of dynamic designs is the focus of the next chapter). Given the high level of abstraction, our structural specification will resemble a domain model, formally describing the file system concepts and their relationships. Another goal of this design exploration is to elicit the set of constraints that characterise a well-formed file system. If later we develop a more detailed specification of the file system, namely of its operations, these would be the constraints we would like to verify to be kept invariant. Our final goal will be to verify that this set of constraints entails other relevant properties of a file system. In particular we are interested in verifying the property that no partitions occur in the file system, meaning that all files and directories are accessible from the root directory.

Signature declaration

First we will declare signatures to capture the concepts in a file system: directories and files. As we have seen in the previous chapter, a signature is a set that groups together some elements of our domain. Since both files and directories share some common properties, namely they can both appear in a directory, it is convenient to declare the respective signatures inside a top-level signature containing all file system objects. To declare a top-level signature we use the keyword sig followed by the signature name and a list of field declarations between braces. For the moment we will not declare fields, so a signature containing all file system objects can be declared simply as follows.

sig Object {}

To declare a subset signature, the keyword in should be used after the signature name, followed by the name of the including (or parent) signature. For example, the two subset signatures of Object containing the directories and files can be declared as follows.

sig File in Object {}
sig Dir in Object {}

In Alloy we typically start validating a design very early in the specification process, when the specification is still quite incomplete. The goal is to find design problems or specification errors as early as possible, and not let them amass to a point where debugging becomes very difficult. For example, we can immediately use a run command to see some instances of our specification so far.

run example {}

A possible first instance returned by this command is the following. Recall that an instance is a valuation of the signatures (and fields, when the specification also declares those) that satisfies all the specified constraints, including the formula between braces in the case of run command. A pair of empty braces is equivalent to true, so in this case we have no constraints imposed on our signatures.

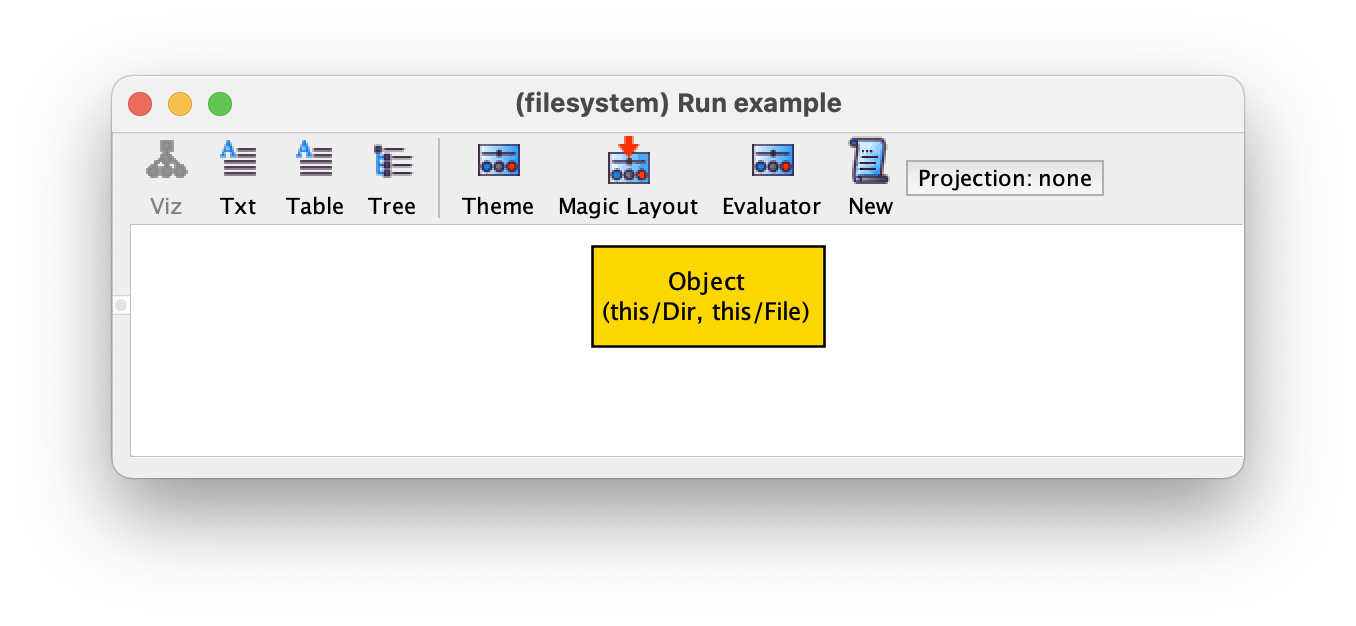
Here we have two objects, one of them is a directory and the other a file. If we press New in the visualizer toolbar we could get the following instance.

Note

Why am I not getting these instances?!

The Analyzer relies on lower level SAT solvers to perform the analysis. Depending on the Analyzer version and the solver you have selected to perform the analysis, you might get instances in a different order than this. You can choose the underlying solver in the Options menu. However, irrespective of the selected solver, if you keep pressing New you will obtain all the possible (non-symmetric) instances of a specification, so you are guaranteed to obtain these. Recall that two instances are considered symmetric (or isomorphic) if they only differ in the naming of the atoms that inhabit signatures.

In this instance we have a single object that is, simultaneously, a directory and a file. Obviously this is not something we wanted, but of course it is allowed since both File and Dir are arbitrary subsets of Object. To disallow this we can add a constraint that forbids an object to be both a file and a directory, by specifying that File and Dir are disjoint sets. To impose this constraint in our specification we can specify it inside a fact, as follows.

fact { no File & Dir }

Recall that & denotes set intersection and no checks for set emptiness.

If we re-execute the example command, and iterate through our instances using New we will no longer see objects that are both files and directories, but we will eventually get an instance such as the following, where we have the problem of having an object (Object0) that is neither a file nor a directory.

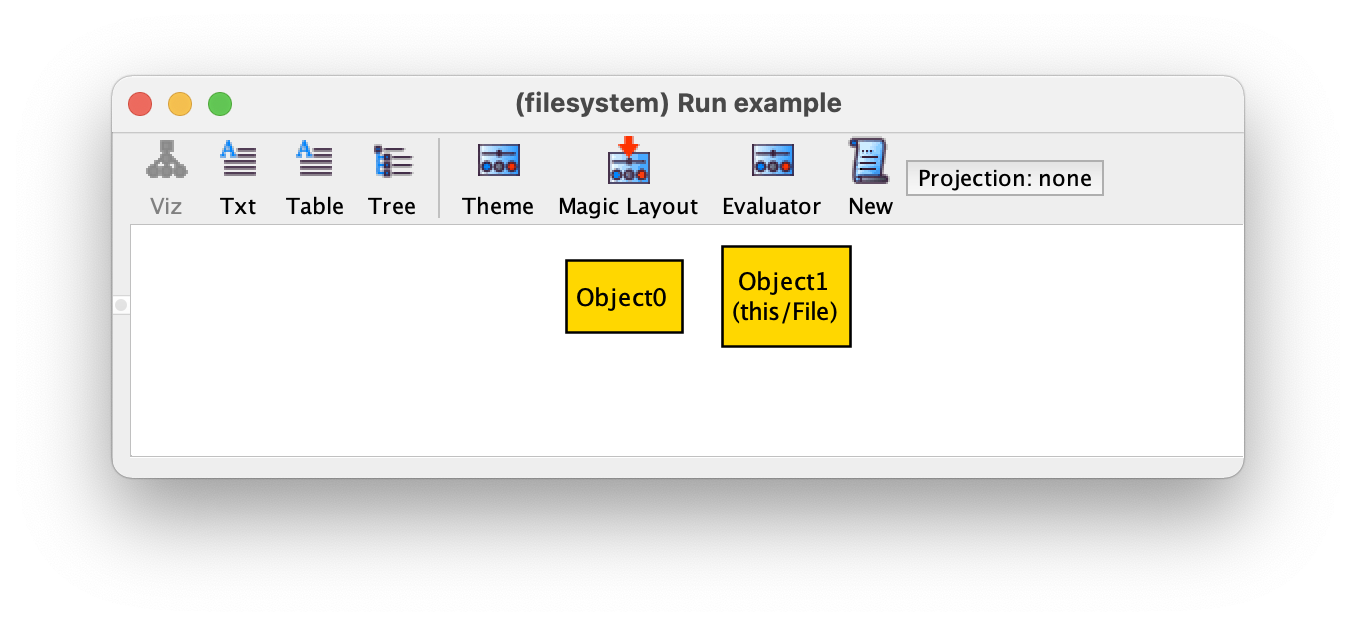
To solve this issue, we can add another constraint to our fact to require that Object contains only atoms in File or Dir, by requiring that Object is the union of both (recall that + denotes set union and that constraints in different lines inside a fact are implicitly conjoined).

fact {
  no File & Dir
  Object = File + Dir
}

By re-executing the example command and iterating through instances we can now confirm that the previous issues appear to be solved.

It is very common to require that some subset signatures are disjoint. Alloy has a special syntax to declare those: instead of in, the keyword extends should be used in the signature declaration. For example, to introduce File and Dir as two disjoint subsets of Object we should declare them as follows.

sig File extends Object {}
sig Dir extends Object {}

The first constraint in our fact is now redundant and can be removed. Actually, we can try to check that indeed it is redundant by issuing the following check command that should yield no counter-example. Recall that a check command verifies that, up to the specified scope, the formula declared between braces is implied by the declared facts. If that is not the case we will get a counter-example instance, one where the facts hold but the formula to be checked doesn’t.

check { no File & Dir }

When executing this command we actually get a warning: the Analyzer refuses to execute the command and tells us that the & operator is irrelevant because the two sub-expressions that it is trying to intersect are disjoint. This is a warning issued by Alloy’s type system and is one of the advantages of using extends to declare disjoint subset signatures, instead of relying on in and additional facts. The main goal of the type system of Alloy is to find so-called irrelevant expressions, essentially expressions that the Analyzer is sure to always denote an empty set and are thus most likely specification errors made by the user. If the user indeed wants to write an expression that always denotes an empty set the special constant none should be used instead, making that intention explicit. More information about Alloy’s type system can be found in [FSE04].

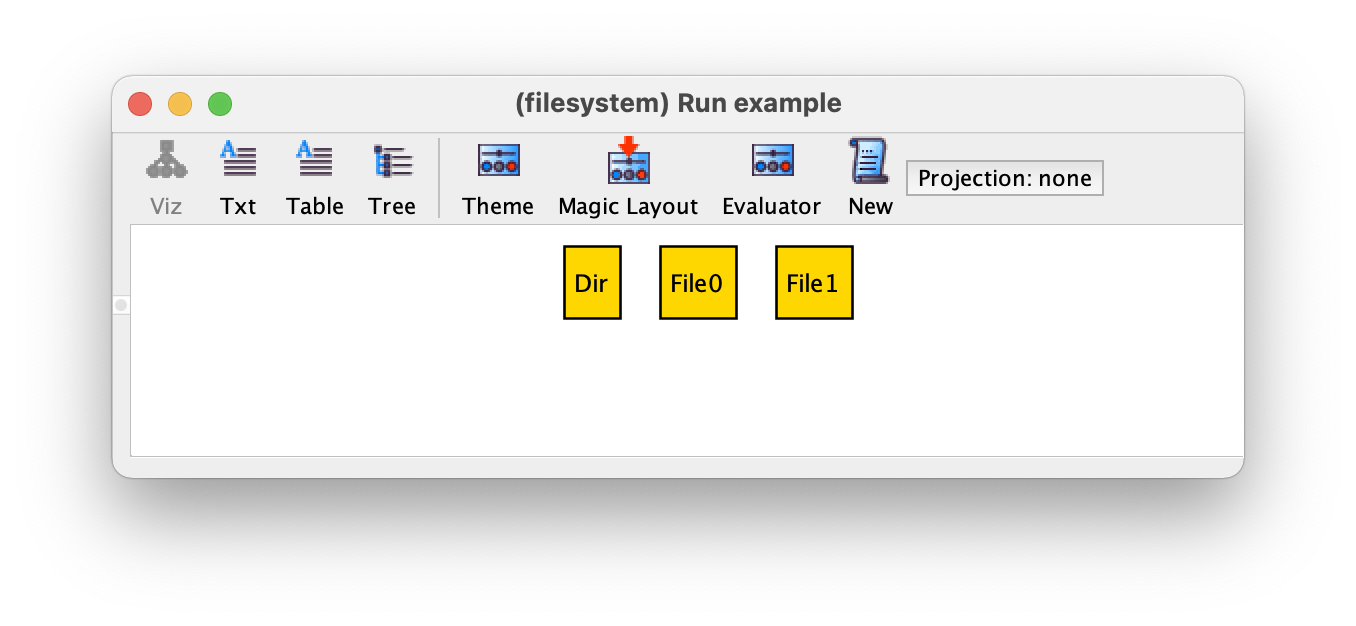
Another advantage of using extends is that in the visualizer atoms will be named according to the most specific signature they belong to, which simplifies the understanding of instances. For example, a possible instance returned by the example command is the following, where it is now more clear that we have two files and one directory.

Another frequent requirement for extension signatures is that they form a partition of the parent signature. This is the case of signature Object, that is partitioned in two sets, File and Dir, and contains no atoms besides those already contained in its extensions. Again, instead of adding facts to ensure this, as we did with the constraint Object = File + Dir, it is possible to declare a signature as abstract, by preceding its declaration with the keyword abstract. Our specification of the file system objects can thus be just as follows, without any need for additional facts.

abstract sig Object {}
sig File extends Object {}
sig Dir extends Object {}

Now we would like to add a special object to denote the directory that is the root of the file system. In Alloy it is not possible in a specification to refer (and name) directly atoms that inhabit signatures. There is however a trick to do so. Signature declarations can be preceded by a multiplicity constraint that restricts the cardinality of that signature. There are three multiplicities that can be used in a signature declaration: some forces the signature to always have some atoms; lone restricts the signature to have at most one atom; and one restricts the signature to have exactly one atom. To have a specific atom for the root directory, we can thus declare with multiplicity one a signature Root that extends Dir.

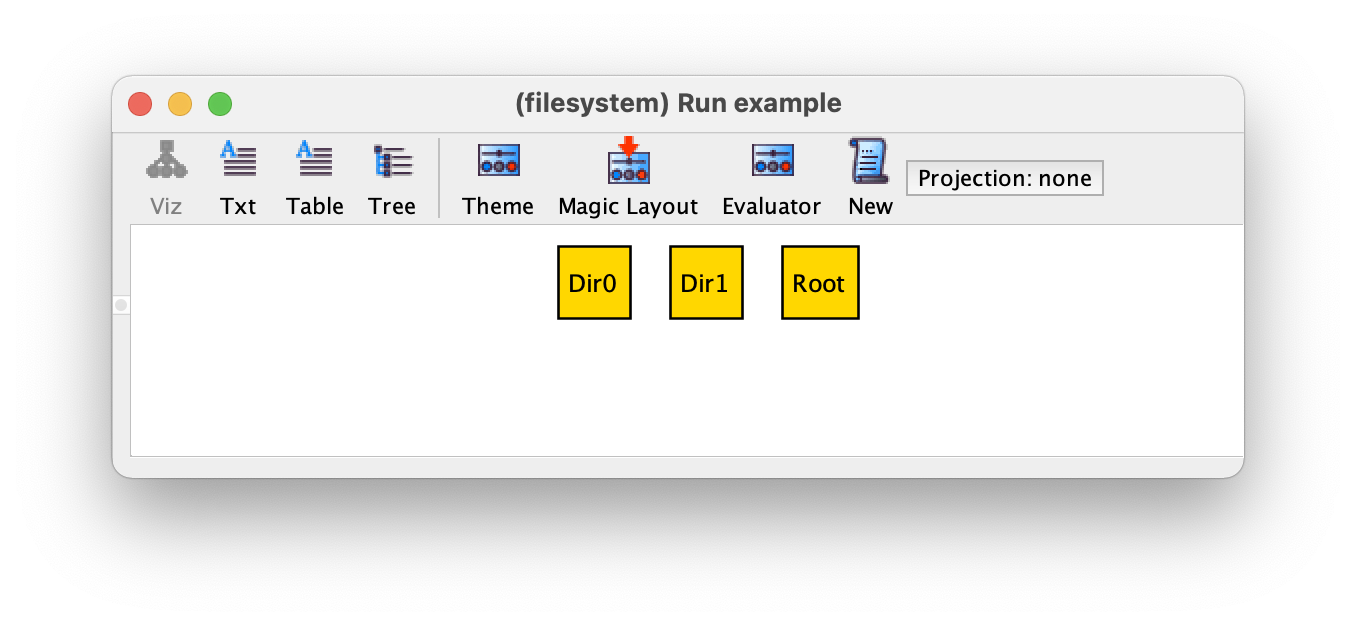
one sig Root extends Dir {}

Root will always be a singleton set that contains the atom that will be the root directory of the file system. Since it is declared with extends, that atom will also be named Root in the instance visualiser. A possible instance returned by the example command is the following, where we have three directories, one of them being (necessarily) the root directory.

Tip

Enumeration signatures.

In Alloy it is very common to use extension signatures of multiplicity one in the declaration of signatures that behave like enumerated data types. For example, the following specification declares a Color signature that contains exactly three colours: Red, Green, and Blue.

abstract sig Color {}
one sig Red, Green, Blue extends Color {}

Here we see another feature of the Alloy language: if two or more signatures share the same features (multiplicity, parent signature, etc) they can all be defined together in the same declaration.

This pattern for declaring signatures that essentially correspond to enumerated data types is so common, that Alloy has a keyword enum for that purpose. Using this keyword, the Color signature could be declared as follows.

enum Color { Red, Green, Blue }

However, there is a subtle difference between declaring enumeration signatures with keyword enum and with the normal sig keyword with multiplicity one: the former additionally imposes a total order between the respective atoms, corresponding to the order in which they are declared inside the braces. Later we will see how total orders can be used in Alloy.

Objects inside directories have an associated name, so we will need a signature to represent the latter. In our file system model we will allow files to be (hard) linked, meaning that the same file can have different names in different directories (or even inside the same directory). As such, we will also introduce a signature Entry that will later be used as a (kind of) record to pack together an object inside a directory and the respective name.

sig Entry {}
sig Name {}

Note

Why not just use strings for names!?

The reader may wonder if Alloy has any predefined types, such as integers or strings. If that is the case, why not just use strings to represent names, instead of declaring a new signature Name? Actually, Alloy does have predefined types, namely Int for (bounded) integers and String for strings. However, these types should be avoided as much as possible, because their semantics is substantially more tricky than that of normal signatures, and analysis can be confusing and somehow crippled when using them (in particular with strings). Actually, in many cases they just have too much semantics for the intended use: for example, strings can be concatenated and there is the notion of one string being a substring of another, but for the file system specification none of this is of interest when specifying the abstract concept of a name. The only thing we will need in this case is to check for name equality, and normal signatures and atoms already provide us that basic semantics. People also tend use integers when they actually need something much more simple, semantics wise. For example, we sometimes need to specify a signature where there is some total order imposed and, in first sight, integers are very convenient for that. However, integers have a more rich semantics than just being a total order, and we can easily axiomatise a total order on a signature with some simple facts and thus avoid the analysis drawbacks that come with their usage (see Working with integers). So, when should you use String or Int? The former has very little use, and actually, even if recognised by the Analyzer, is not even part of standard Alloy. The latter is sometimes useful, for example when you do need to perform arithmetic operations, such as additions or subtractions.

A possible instance of our specification so far is the following, with two different names, two entries, one file and two directories, one of which is the root.

Recall that all analysis commands are executed with a (user definable) scope for each signature, that sets the maximum number of atoms that can inhabit it. By default, the scope is 3 for all top-level signatures: in our example this means that instances will have at most 3 names, 3 entries, and 3 objects. With this scope, instances with, for example, 3 files, will not be possible, because the root always exists and consumes 1 of the 3 atoms that can inhabit Object. To change the default global scope the keyword for followed by the desired scope should be used. You can also set a different scope for each top-level or extension signature (another difference from declaring signatures with in), by using the keyword but followed by a comma separated list with different scopes for each signature. You can also set an exact scope for a signature with the keyword exactly, meaning that that signature will always be inhabited by the exact number of specified atoms. For example, to execute the example command with a default scope of 4, up to 2 entries, and exactly 3 names, the scope should be set as follows.

run example {} for 4 but 2 Entry, exactly 3 Name

Note that in this case, the only top-level signature that will be subject to the default scope of 4 is Object, since specific scopes are given for the other two top-level signatures. Multiplicities on signature declarations also affect the scope: for example, a signature with multiplicity one will always have scope of exactly 1, and an error will be thrown if you try to set an incompatible scope. There is also some interaction between the scope of extension signatures and the scope of the respective parent signatures. In particular, if the scope of extension signatures enforces a minimum number of atoms, the scope defined for the parent signature will automatically grow to accommodate that minimum number. For example, in the following command the scope of Object will automatically grow to 4 since Object must contain at least the root and three files.

run example {} for 3 but 2 Object, exactly 3 File

Field declaration

Having declared our signatures we now proceed with the declaration of fields. Fields are declared inside the braces of a signature declaration, and are essentially mathematical relations (sets of tuples) that connect atoms of the enclosing signature to other atoms (of the same or other signatures). In our example we will need a relation that connects each directory with the respective set of entries. This binary relation, which will be named entries, is a set of ordered pairs, where the first atom of each pair is a directory and the second atom is an entry. The type of the first atoms in the tuples that form a relation dictates the signature in which it must be declared as a field. In the case of entries, since it relates atoms of signature Dir to atoms of signature Entry, it must be declared as a field in the former signature. To do so, we change the declaration of Dir as follows.

sig Dir extends Object {
  entries : set Entry
}

As we can see, a field declaration consists of its name followed by a colon and the target set, optionally preceded be a multiplicity declaration. In this case the target set is signature Entry and the multiplicity is set, meaning that one atom of signature Dir can be related by entries to an arbitrary number of atoms of signature Entry. The other options for the multiplicity are the same that can be used in signature declarations: one, lone, or some. If no multiplicity is given, the default is one. In this book we will avoid this implicit multiplicity in field declarations, and always explicitly state the multiplicity of a field, even if it is one.

By executing command

run example {}

we could now get the following instance.

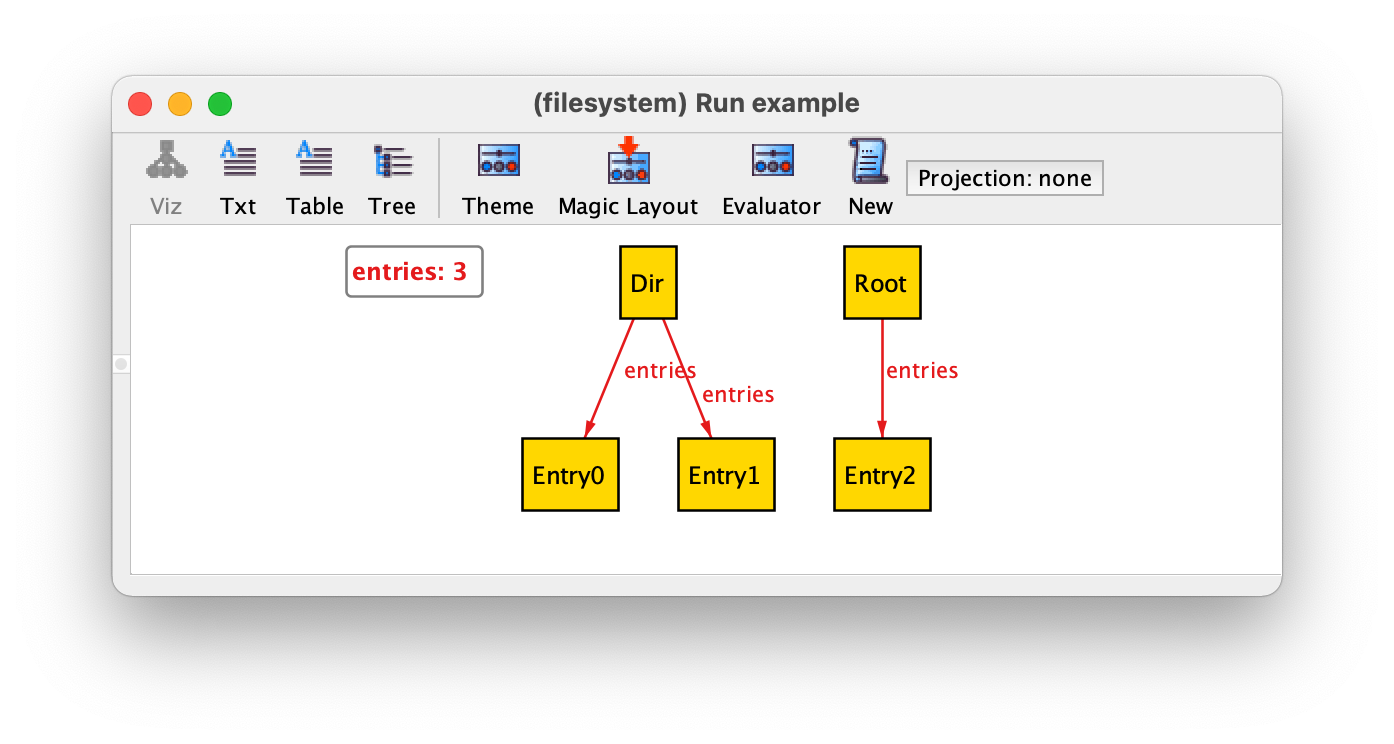
Binary relations are depicted by the Analyzer using labelled arrows: each arrow is a pair contained in the relation, whose first atom is the source of the arrow and whose second atom is the target. In this case, relation entries is a set that contains three pairs: (Dir,Entry0), (Dir,Entry1), and (Root,Entry2). In this example we have a directory Dir with two entries and the Root with one entry, but given the set multiplicity constraint it would also possible to have directories without any entries.

Note

Actually, everything is a relation!

In chapter An overview of Alloy we alerted the reader to the fact that in Alloy every expression denotes a set. To be more precise, every expression in Alloy denotes a relation - a set of tuples - hence the Alloy motto: everything is a relation! In Alloy we can declare relations of arbitrary arity: the arity is the size of the tuples contained in it. Relation entries is a binary relation of arity 2. Later we will see how to declare relations of higher arity, for example ternary relations of arity 3. However, signatures are in fact also relations of arity 1: they are sets of tuples of size 1. For example, in the previous instance, signature Dir contains the following unary tuples: (Dir) and (Root). Do not to confuse the name of the atom Dir with the signature name Dir: the former is just an automatically-generated name for one of the two inhabitants of the latter! When we start using relational logic operators to write constraints, it will be more clear why the fact that everything denotes a relation considerably simplifies the syntax and semantics of the language.

Tip

The evaluator.

The Alloy instance visualiser has an evaluator that can be used to compute the value of any expression. To access this evaluator just press the Evaluator button in the toolbar of the instance visualiser window. Every expression denotes a relation. The visualiser depicts the values of the signatures and fields of an instance as labelled graphs. Another way to depict the value of a relation (of any arity) is as a table where each line is one of the tuples contained in it. This is the default way the evaluator will show the values of relational expressions. To ask for the value of an expression just type it in the evaluator and press Enter. For example, here is the result of asking in the evaluator what is the value of relations Dir and entries.

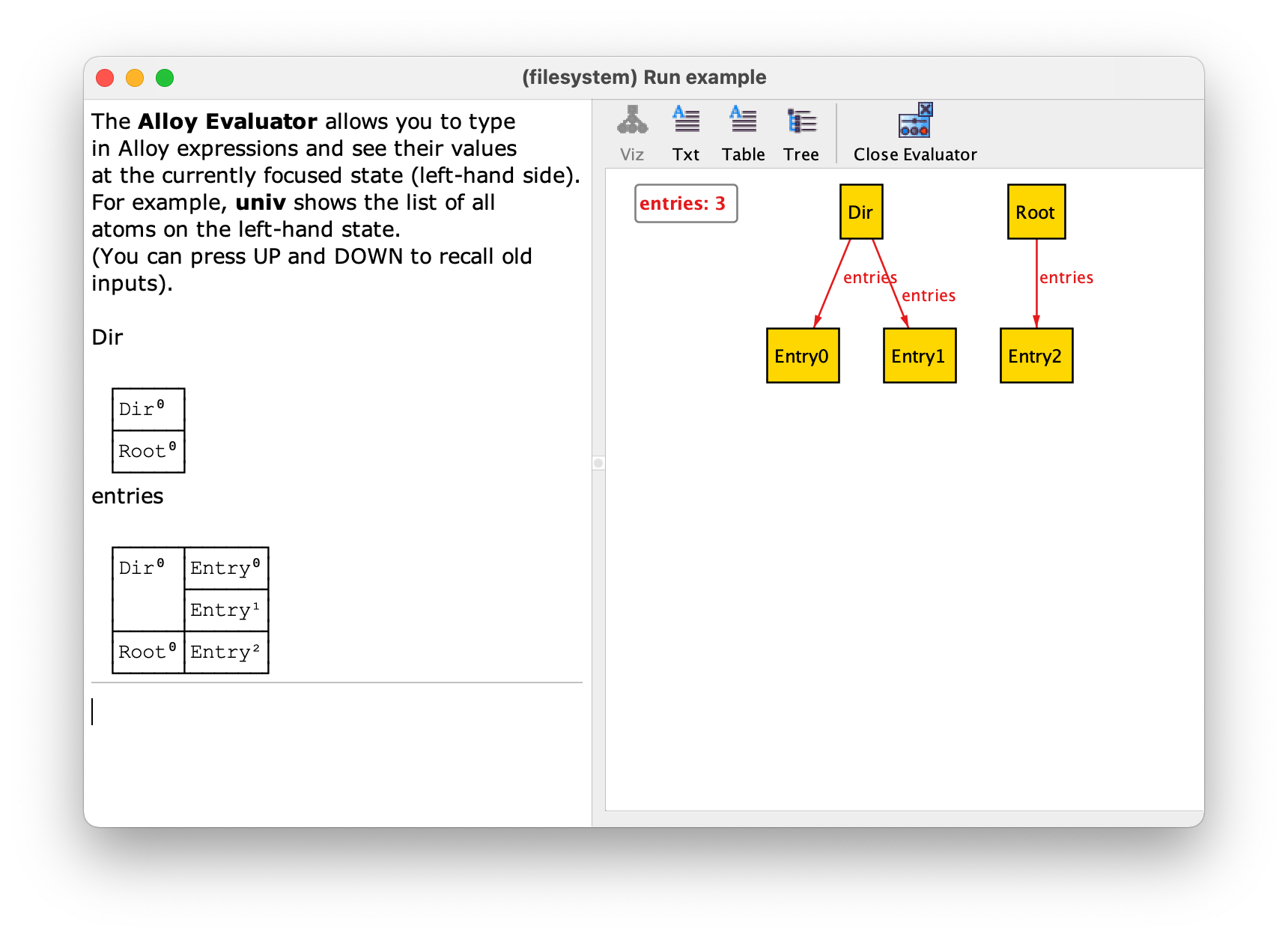
The evaluator is sometimes very useful to debug your constraints: besides asking for values of relational expressions you can also ask for the values of formulas, so it is a very convenient way, for example, to know what sub-formulas of a constraint are true or not in a particular instance. To close the evaluator and return to the normal instance visualizer just press the Close Evaluator button in the toolbar. Section Using the evaluator to debug specifications presents the evaluator in more detail.

Besides entries we will declare two more fields in our specification: the first, that we will call name, relates each entry in a directory with the respective name; the second, that we will call object, relates each entry in a directory with the respective file system object (either a file or a directory). Both these relations should be declared inside signature Entry and both will have multiplicity one, since exactly one target atom is associated with each entry. Because of this, an entry acts like a record that packs together an object inside a directory and the respective name. In section Using higher-arity relations we will see how this association (between directories, their contents, and the respective names) can alternatively be modelled by a ternary relation.

sig Entry {
  name : one Name,
  object : one Object
}

Let’s change our run command to ask directly for a more complex instance of our specification, namely one with a larger global scope of 4, and necessarily containing some files and some directories besides the root (recall that - is the set difference operator, and that keyword some, besides being used as a multiplicity constraint in declarations, can be used in formulas to check if a set (or relation) is non-empty).

run example {
  some File
  some Dir - Root
} for 4

Executing this command could yield the following instance.

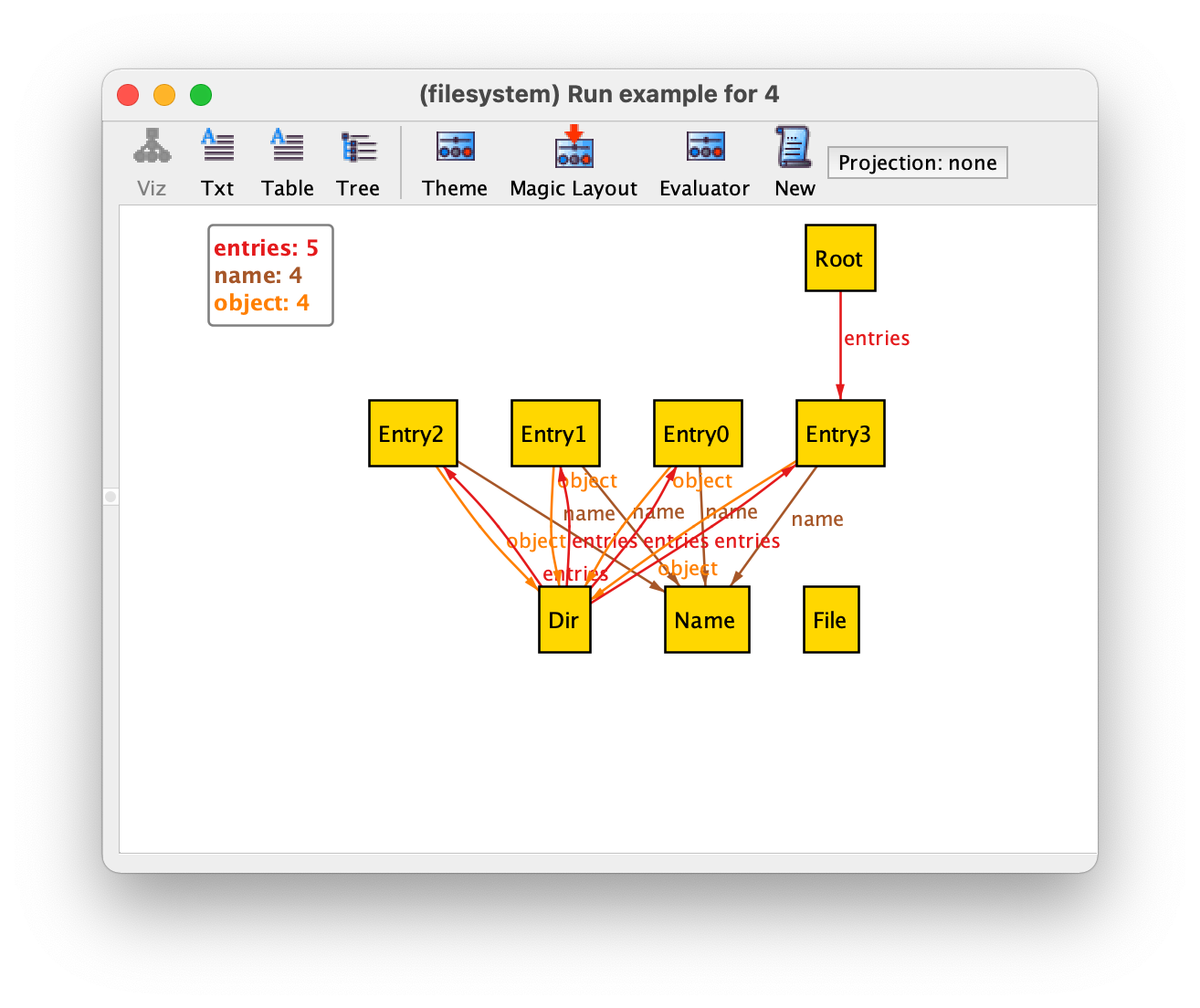
Here we can immediately see some problems with our specification, for example entries shared between directories or files not belonging to any directory. As our specification grows, instances become increasingly difficult to understand, and so, before adding facts to our specification to solve these issues, we will first see how the theme can be customised to simplify the visualisation of instances.

Theme customisation

To open the theme customisation menu, press the button Theme in the toolbar of instance visualiser window. The first customisation we will apply is to show the names of directory entries as attributes in the respective atoms, instead of using arrows pointing to the name. This will unclutter substantially the depiction and is a very common customisation for fields of multiplicity one, in particular for fields that somehow act as identifiers, as is the case of name. To do so, first select the field name, and then tick the Show as attribute option in the top pane. This option will show the name of an entry as an attribute but still keep the respective arrows. To remove them, tick twice Show as arcs to choose the Off option. Your theme options for relation name should look as follows.

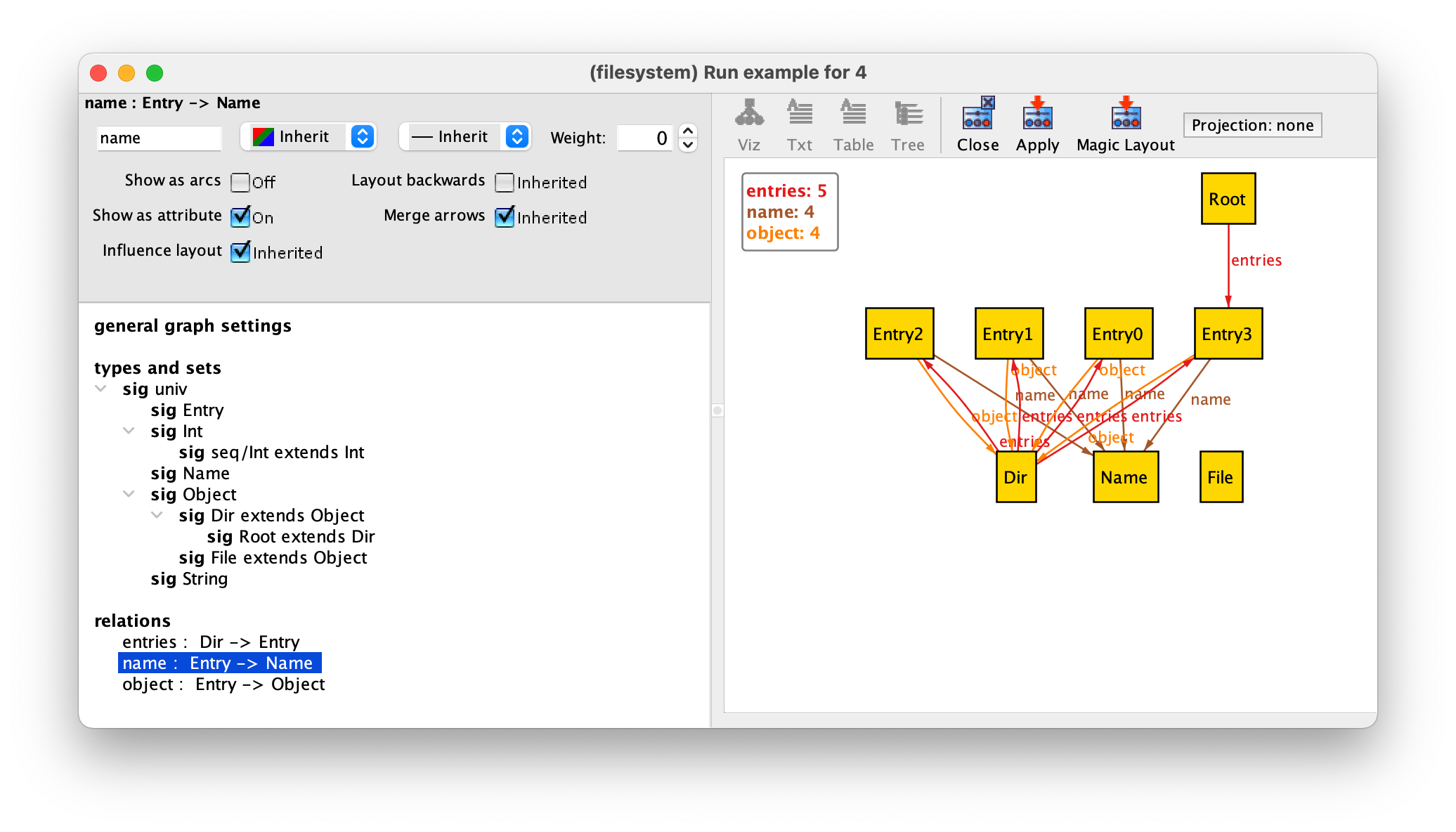
By pressing Apply in the toolbar and then Close the instance will now be depicted as follows.

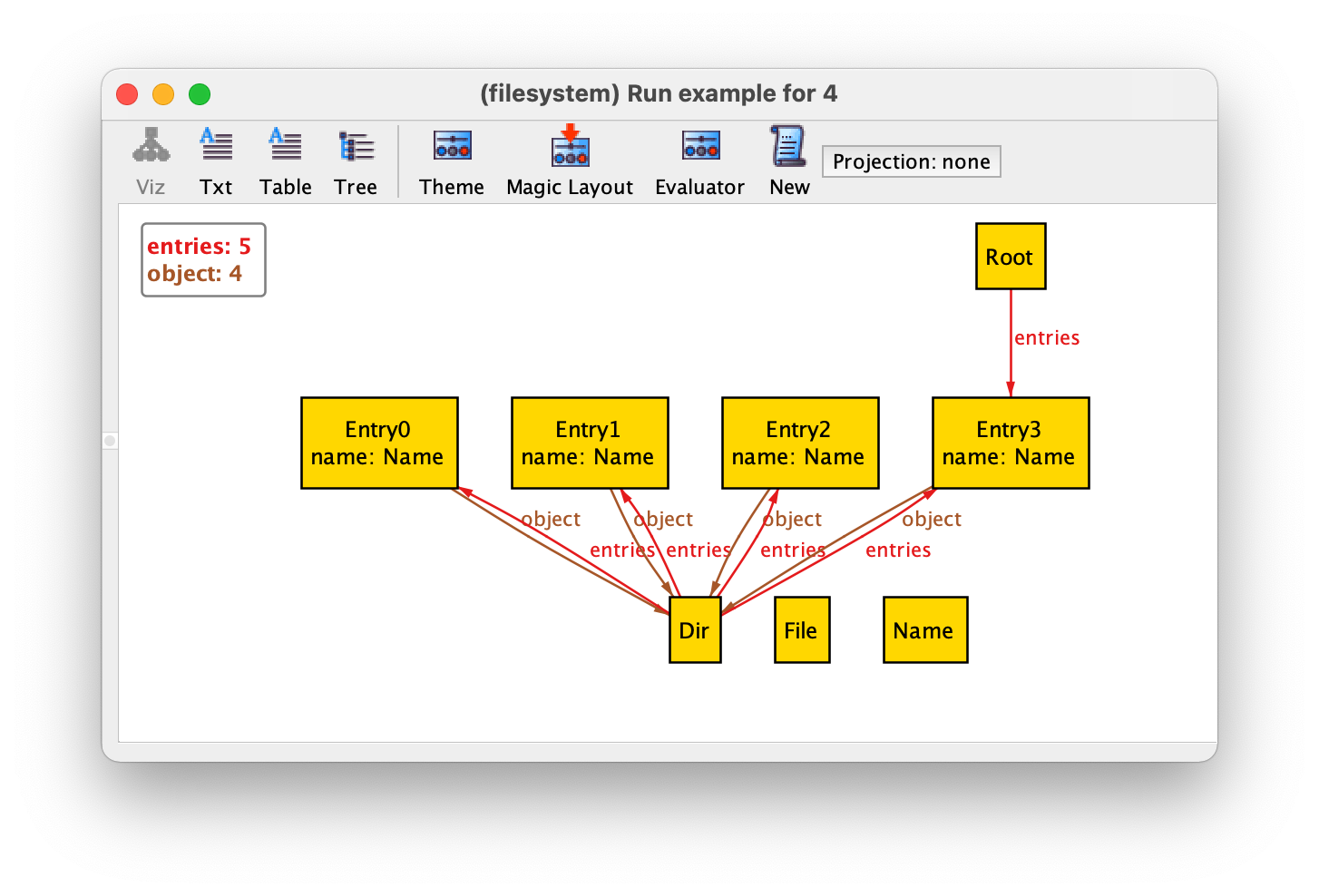
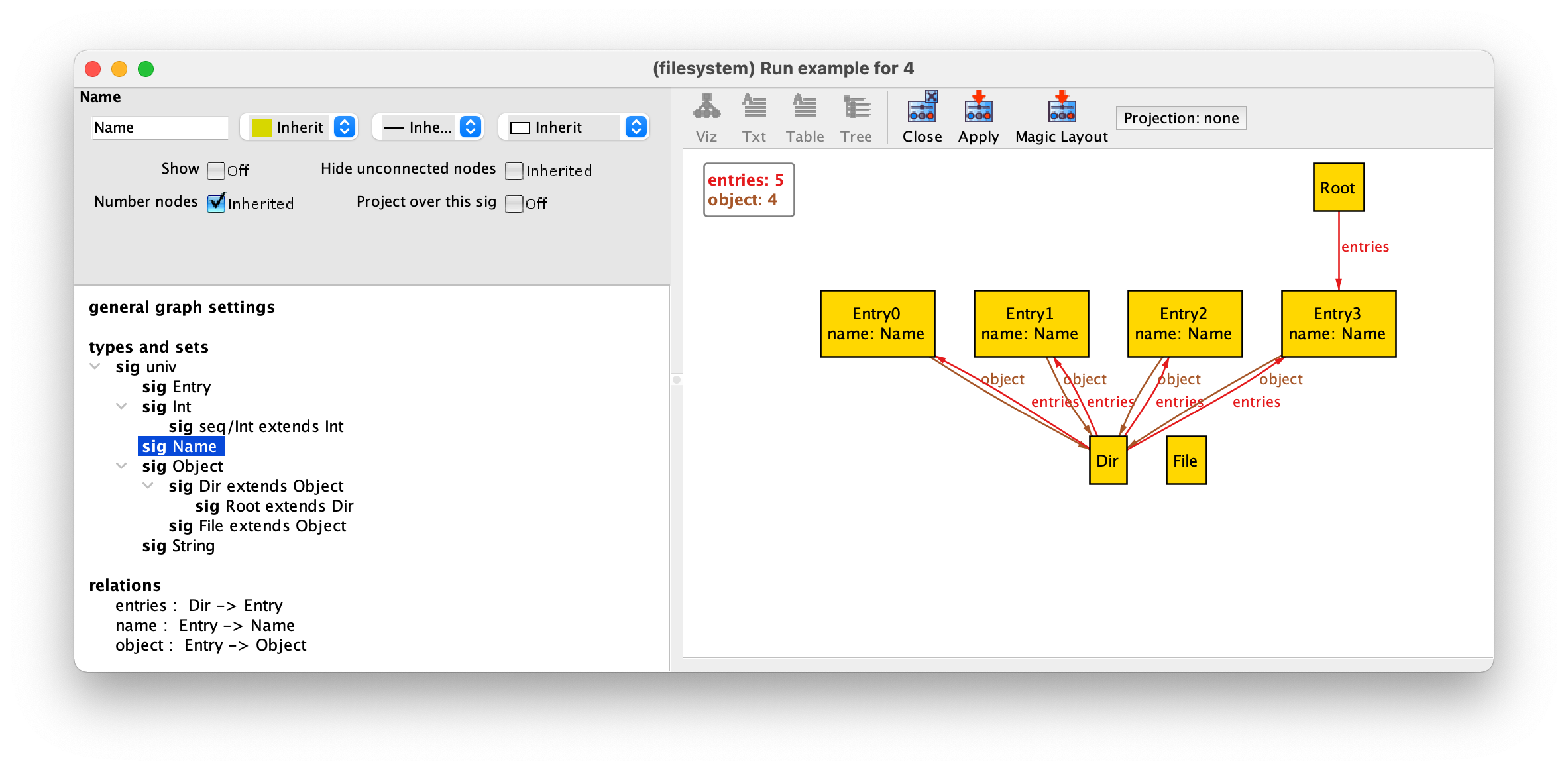
We now have some unconnected Name atoms. Since names were only used in directory entries, where they are now shown as attribute, we can remove them from the graph. To do so, select Theme again (actually when changing many options it is better to keep the theme customisation menu open and just keep pressing Apply without closing it to see the effect), select the Name signature, and then tick the Show option twice to choose the Off option. After pressing Apply the Name atom will disappear.

Another common customisation is to give different colours (or different shapes) to atoms belonging to different signatures. First, we will select a different colour palette, with more subdue colours. First select the general graph settings, and select the Martha (for Martha Stewart) palette both for node and edge colours. After pressing Apply we will get some nice faded colours.

Since entries are auxiliary structures in defining the (supposedly) tree-like structure of the file system, we will paint them grey. To do so select signature Entry, then the colour Gray in the drop-down menu in the top left-hand corner, and finally Apply.

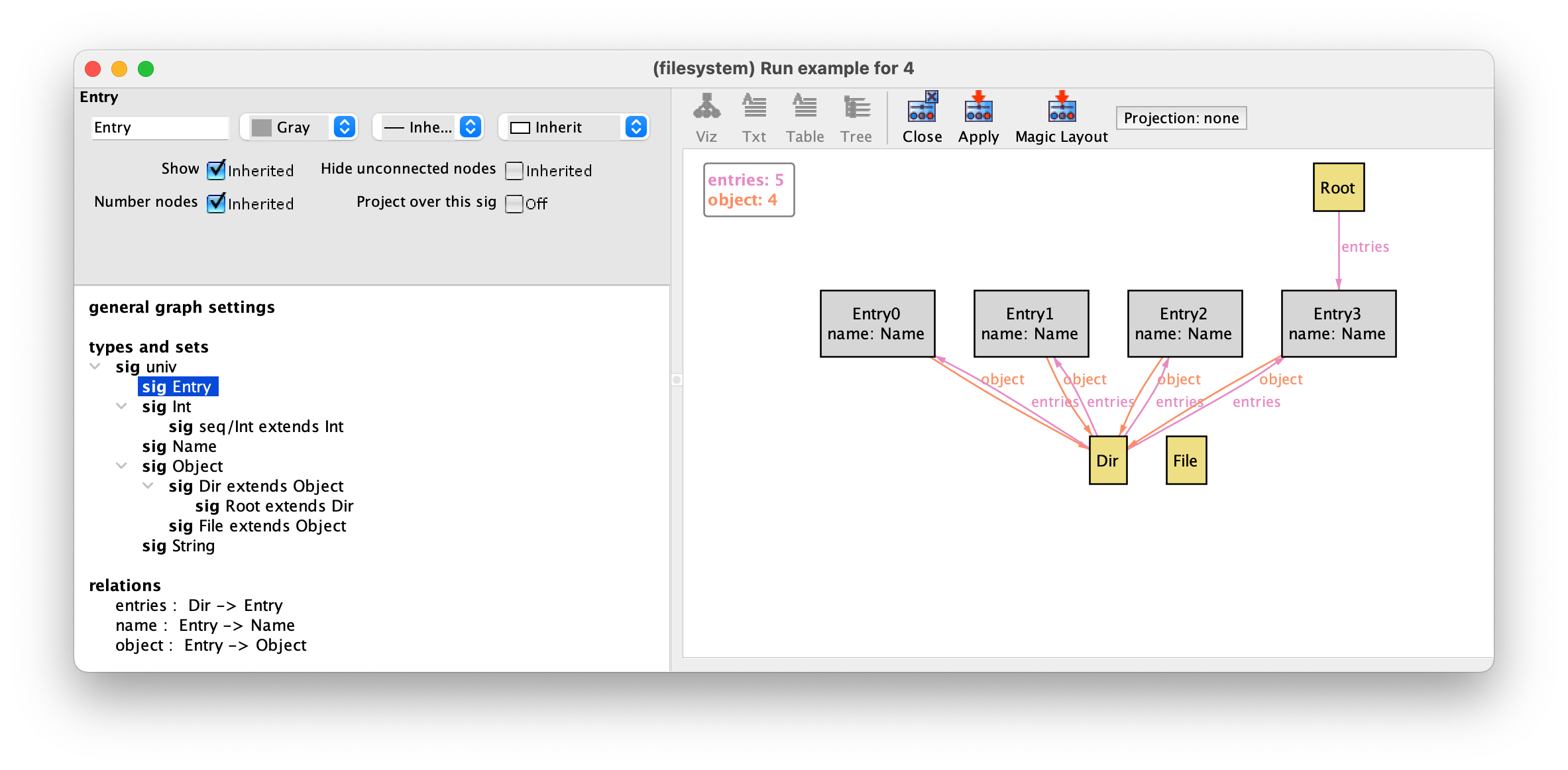
For file system objects we will choose a more eye-catching red colour. We don’t have to set this colour separately for Dir and File. By default most theme options of extension signatures are set as inherited from their parent signature. As such, it suffices to set the colour red for the Object signature, and both their children will inherit this setting. Finally we will choose different shapes for different file system objects. Let’s keep files as rectangles, but choose the shape Trapezoid for directories and a House for the root. The shape can be chosen in the drop-down menu in the top right-hand corner. After pressing Apply we have the following visualization.

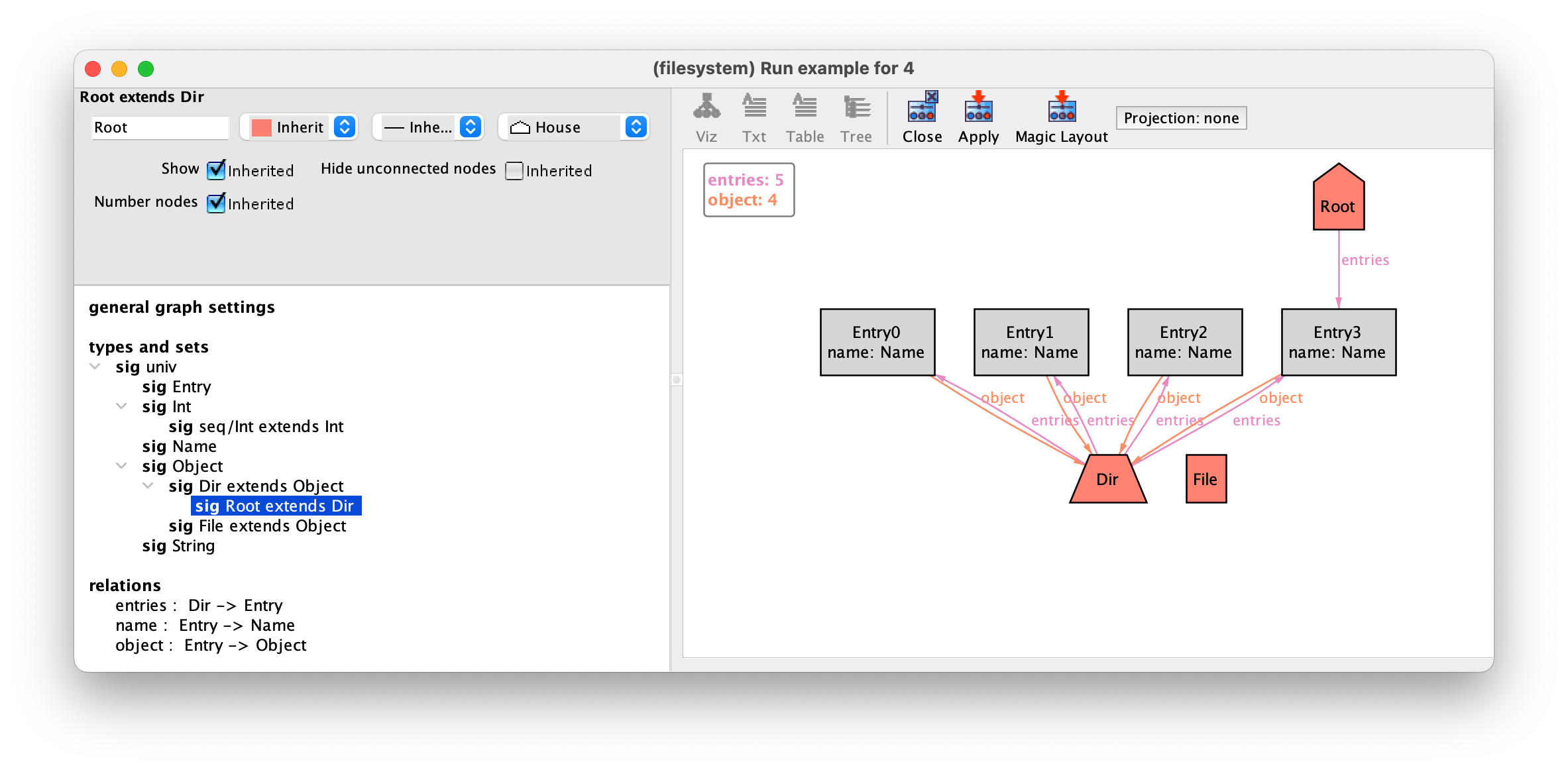
For the moment these are all the customisations we will use, and so we can close the theme customisation menu. Notice that you can always reset your theme settings by going to the menu option Theme ‣ Reset theme. You can also save your theme for later use in the option Theme ‣ Save theme.

Instead of customising manually your theme, you can also try out the Magic Layout button in the toolbar of the instance visualiser. This will “magically” choose options for visualising the different elements of your specification: sometimes the results are good enough and it will save you some work. The result of magic layout for our instance is the following.

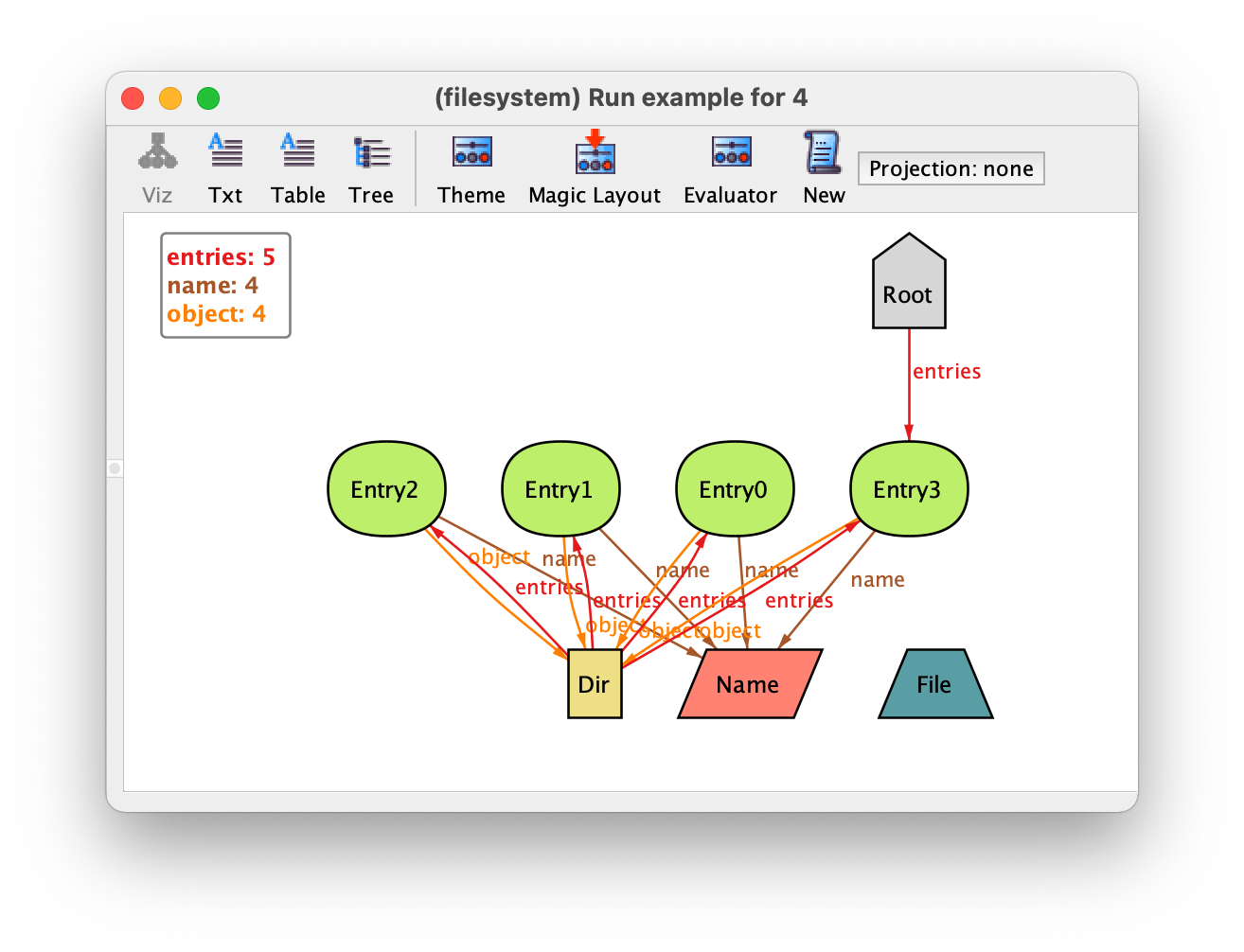
More information about how the magic layout actually works can be found in [LED07]. In this case we prefer our handmade customisation and so we will load back our previously saved theme by selecting Theme ‣ Load theme.

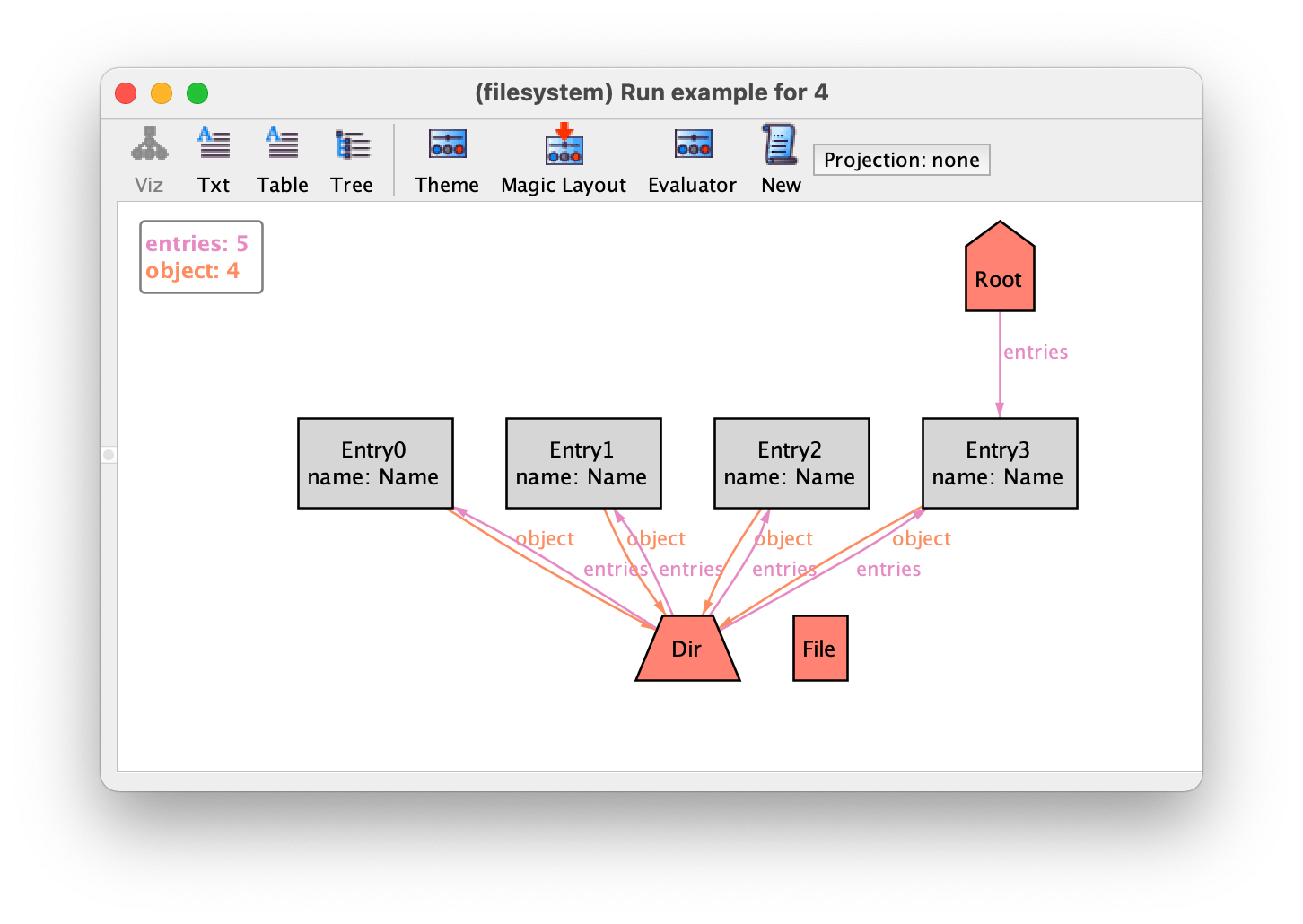
Property specification

By inspecting the above instance we can easily detect several problems in our specification, namely:

• Shared entries between directories (entry Entry3 belongs both to Dir and Root).

• Different entries in the same directory with the same name (all entries inside Dir have the same name Name).

• The same directory appears in more than one entry (Dir is the object of all entries).

• A file that does not belong to an entry (File)

We should write facts to prevent these issues. In Alloy, formulas in facts are written in a variant of first-order logic called relational logic. Relational logic extends first-order logic with so called relational operators, that can be used to combine (or compose) relations (which in first-order logic are known as predicates) to obtain more complex relations. We have already seen some of these operators, namely the classic set operators such as intersection (&), union (+), and difference (-). Notice that every relation (of any arity) is a set of tuples, so these can be applied to any relation. Let’s suppose, for example, we have two binary relations, mother and father, that relate a person with the respective mother and father. Then the relation that gives the parents of a person can be obtained by taking the union of both, namely mother+father.

The essential operator in relational logic is composition, the binary operator written as . (a dot). This operator allows us to navigate through the declared fields to obtain related atoms. Understanding how this operator works is key to be proficient in Alloy. Here, we will explain its informal semantics by means of several examples: the detailed semantics and more examples will be given in chapter A relational logic primer. In particular we will focus on the simplest, and most frequent, use of this operator, namely when applied to a set and a binary relation. For example, suppose e is a singleton set containing an Entry and d a singleton set containing a Dir. These could be, for example, parameters of a predicate or instantiated as result of a quantifier. To obtain the name of an entry you can compose it with relation name: relational expression e.name denotes the name of e. Since name is a field with multiplicity one, the result of this composition is necessarily a singleton set. Similarly, e.object is the singleton set with the file system object that is contained in entry e.

The notation is, on purpose, similar to that of accessing an attribute of an object in an object-oriented programming language, as the effect is essentially the same when dealing with singleton sets. However, we can also apply it to relations with multiplicity different than one and arbitrary sets. For example, d.entries retrieves the set of all entries in directory d. This set can be empty or contain an arbitrary number of entries, since relation entries has multiplicity set. A more interesting usage is when composing a non-singleton set with a relation. For example, Entry.name is the set of all names of all entries and Dir.entries is the set of all entries that belong to some directory. Also, you are not forced to compose a set followed by a relation: the other way around also works. Relations can be navigated forwards, from the source signature to the target signature, but also backwards from the target signature to the source one. For example, entries.e denotes the set of directories that contain entry e: this set can be empty, if e is not contained in any directory, or even have more than one directory, since when declaring a field there are no multiplicity restrictions imposed on the source signature. We can also compose with an arbitrary set on the right-hand side: for example, entries.Entry is the set of all directories that contain some entry.

Compositions can be chained to obtain atoms that are somehow indirectly related. For example, d.entries.object denotes the set of all file system objects that are contained in the entries of directory d. And again, it is possible to navigate backwards through composition chains. For example, entries.object.d denotes the set of all directories with entries that contain directory d.

Having understood how . works, we can now declare a fact that prevents the first issue identified above. We can almost directly transliterate the natural language requirement to relational logic. Given any two different directories x and y, the property that there should be no common entries between both can be specified as no (x.entries & y.entries): first we determine the intersection of the two sets of entries of both directories, and then we check that this set is empty using the keyword no. To complete our first property specification we just need to universally quantify over all different directories x and y (recall that all denotes the universal quantification of first-order logic).

fact {
  // Entries cannot be shared between directories
  all x, y : Dir | x != y implies no (x.entries & y.entries)
}

The need to quantify over two ore more different variables is very common, so Alloy provides the modifier disj, that can be added between the quantifier and the variables, precisely to restrict those variables to be different. This modifier simplifies the formulas, since we no longer need the implication to indirectly restrict the range of the quantification. Using this modifier, our property can be restated as follows.

fact {
  // Entries cannot be shared between directories
  all disj x, y : Dir | no (x.entries & y.entries)
}

As expected there are many different ways to specify the same property. In the case of this property, a simpler formula can be obtained by navigating backwards in the entries relation, and specifying instead that for every entry e there should be at most one directory in the set entries.e, the set of all directories that contain e as an entry. This alternative formulation would look as follows. Recall that lone can be used to check if a set contains at most one atom.

fact {
  // Entries cannot be shared between directories
  all e : Entry | lone entries.e
}

Alloy has a special formula syntax to directly restrict the multiplicities of both end points of a binary relation. For example, to state that a relation r relates every atom of source signature A to at most one atom of target signature B, and every atom of B to at least one atom of A, we could write the formula r in A some -> lone B. Not stating a multiplicity next to an end point is the same as having multiplicity set. With this special syntax, we could have yet another alternative formulation of our first constraint.

fact {
  // Entries cannot be shared between directories
  entries in Dir lone -> Entry
}

Note

A bestiary of binary relations.

The constraint entries in Dir lone -> Entry forces relation entries to be injective, one where no two atoms of the source signature point to the same target atoms. This is one of the four basic properties of relations we can obtain by varying the multiplicities of the source and target signatures. If we had entries in Dir some -> Entry we would have a surjective relation, one where every atom of the target is related to some source atom. If entries in Dir -> lone Entry relation entries would be simple (or a partial-function), a relation where every source atom is related to at most one target. And if entries in Dir -> some Entry relation entries would be entire (or total), since every source atom is related to at least one target. By combining these four properties we get additional well-known relation types. A relation that is both entire and simple is a function: every atom of the source is related to exactly one target. A representation is a relation that is both entire and injective, and dually, an abstraction is a relation that is both simple and surjective. An injection is a function that is also a representation, and a surjection is a function that is also an abstraction. Finally, by combining all four basic properties we get a bijection: a one-to-one mapping between the source and the target signatures. The following table summarises these properties.

injective	entire		simple		surjective
A lone -> B	A -> some B		A -> lone B		A some -> B
representation		function		abstraction
A lone -> some B		A -> one B		A some -> lone B
injection			surjection
A lone -> one B			A some -> one B
bijection
A one -> one B

To enforce that different entries in the same directory have different names we could write the following fact.

fact {
  // Different entries in the same directory must have different names
  all d : Dir, disj x, y : d.entries | x.name != y.name
}

Here you can see another nice feature of Alloy’s syntax: it is possible to quantify over any expression and not only over signatures. In this case, x and y will be instantiated with all the (distinct) atoms belonging to d.entries, the set of entries of each directory d. An alternative formulation of this property is the following.

fact {
  // Different entries in the same directory must have different names
  all d : Dir, n : Name | lone (d.entries & name.n)
}

Expression d.entries & name.n denotes the set of entries in directory d that also have name n. This set must contain at most one entry for every directory d and name n.

To prevent the third issue we can enforce that each directory is contained in at most one entry as follows.

fact {
  // A directory cannot be contained in more than one entry
  all d : Dir | lone object.d
}

Note that it would be wrong to specify this property as object in Entry lone -> Dir, since this would force relation object to only relate entries to directories (excluding files).

The last issue is a an example of a broader problem: there is nothing in our specification that forces all objects except the root to belong to an entry. To specify such a constraint, we can begin by determining the set of all objects that are contained in any entry using expression Entry.object, and then enforce that this set is equal the set of all objects minus the root.

fact {
  // Every object except the root is contained somewhere
  Entry.object = Object - Root
}

After adding these four facts, if we re-execute the example command and iterate with New we could get the following instance.

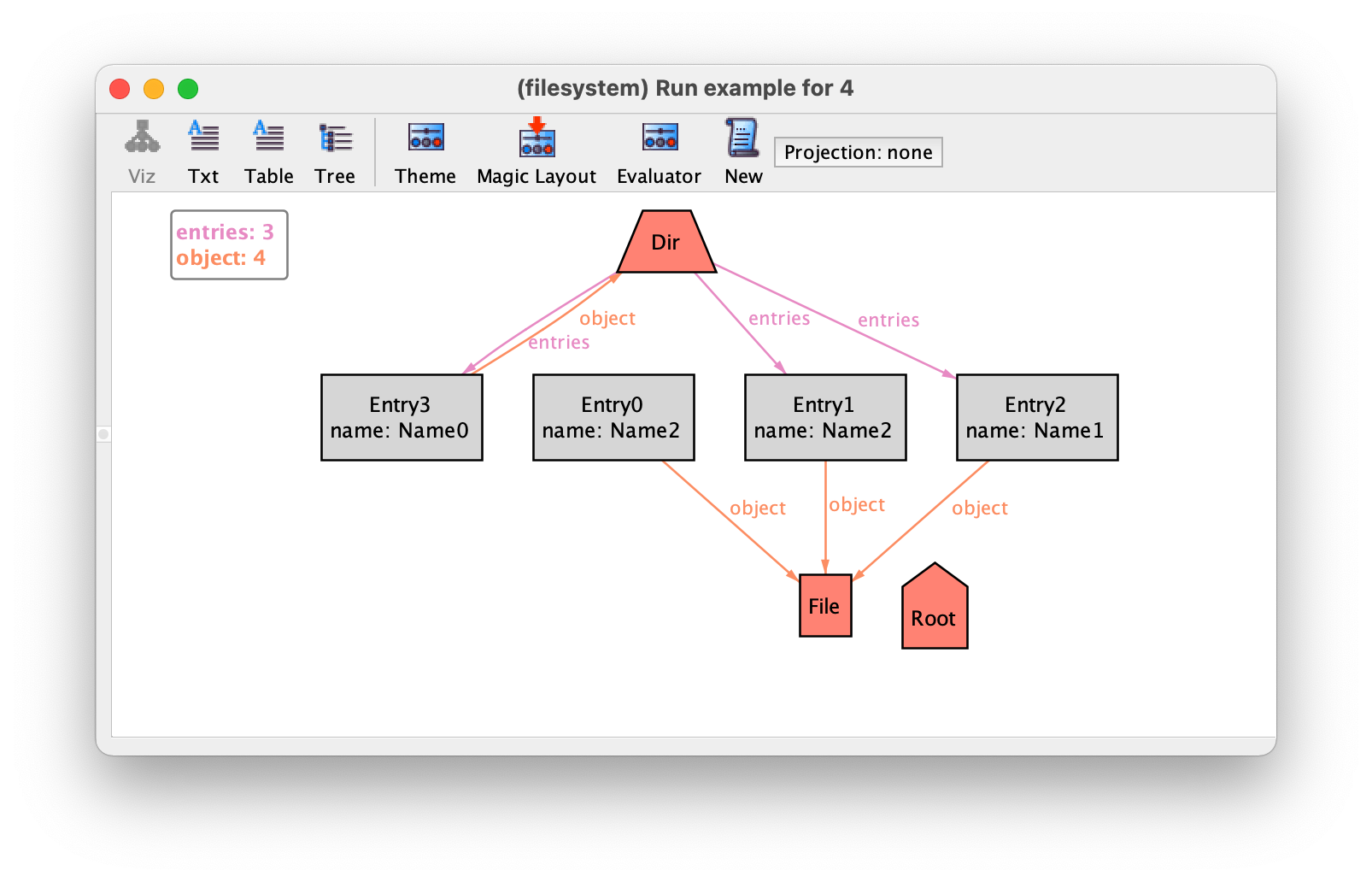
The problems identified above are now gone, but we still have two issues (the second already present in the previous instance):

• Entries not belonging to any directory.

• Directories contained in themselves.

To address the first issue we could just strengthen the first fact introduced above to demand that every entry belongs to one and exactly one directory.

fact {
  // Entries must belong to exactly one a directory
  entries in Dir one -> Entry
}

Concerning the second issue, to forbid directories from containing themselves as entries, we can use the previously described expression d.entries.object to determine the objects contained in a directory d. Then we just need to forbid d itself from being a member of this set.

fact {
   // Directories cannot contain themselves
   all d : Dir | d not in d.entries.object
}

Re-executing again command example and iterating a couple of times with New reveals no more issues. Obviously, it is impossible to manually inspect all possible instances, so we will proceed with the verification of our desired assertion, namely that the file system contains no partitions.

Assertion verification

To specify this assertion we need to determine the set of all objects that are reachable from the root. We have already seen how to determine the set of objects that are directly contained in a directory. Namely, Root.entries.object is the set of objects directly contained in the Root directory. The set of objects reachable from Root contains not only these, but also the objects that they contain, which can be determined as

Root.entries.object.entries.object

Of course, we also need to include the objects contained in these, and so on, and so on. Essentially, we would like to determine the following set:

Root.entries.object +
Root.entries.object.entries.object +
Root.entries.object.entries.object.entries.object +
...

The problem is how to fill in the ... in this expression: ultimately the number of times we need to compose entries.object depends on the size of our file system, and we would like our specification to be independent of this value. Fortunately, relational logic includes a so-called transitive closure operator (^) that when applied to a binary relation (or relational expression) determines the binary relation that results from taking the union of all its possible compositions. Essentially, given a relation r, ^r is the same as r + r.r + r.r.r + .... Seeing our instances as labelled graphs, the expression x.^r will determine the set of all atoms that can be reached from atom x by navigating in one or more steps via arrows labelled with r. Transitive closure is the reason why relational logic is strictly more expressive than first-order logic: our desired assertion could not be expressed in first-order logic alone.

By using transitive closure applied to relational expression entries.object we can determine the set of all objects reachable from root. To ensure that there are no partitions, this set must contain all objects (except the root itself). Our desired assertion can thus be specified as follows.

assert no_partitions {
  // Every object is reachable from the root
  Object - Root = Root.^(entries.object)
}

To verify that this assertion is a consequence of all the facts that have been imposed before, we can define a check command.

check no_partitions

Unfortunately, executing this command reveals a counter-example.

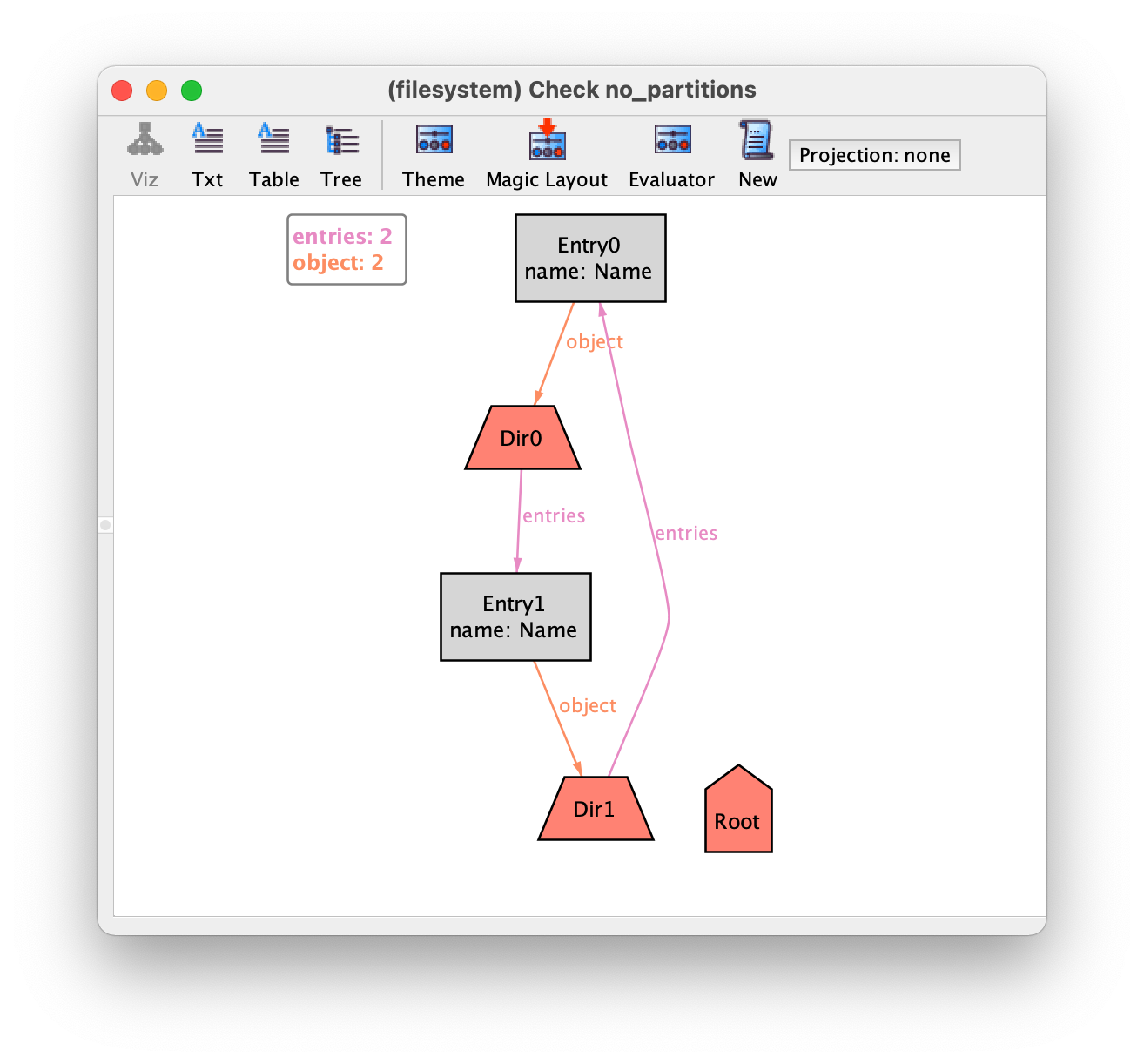
The problem is that we have two directories that contain each other. Fortunately, this counter-example is not an issue in real file systems, but exposes a problem in our specification. One of the facts specified above imposed that no directory can contain itself, but this alone is not sufficient: a directory cannot contain itself directly, nor indirectly. To fix that fact, we can again use the transitive closure operator to determine the set of all objects reachable from any directory d, and then disallow d from being a member of this set.

fact {
   // Directories cannot contain themselves directly or indirectly
   all d : Dir | d not in d.^(entries.object)
}

Re-executing the check command no longer yields counter-examples. Although with the bounded analysis performed by the Analyzer we can never be entirely sure that the assertion is valid, we can set a higher scope to increase our confidence that that is indeed the case.

check no_partitions for 6

Tip

Be sure your specification is still consistent!

You should always be wary of the results of checking your assertions, in particular when they yield no counter-examples. Recall that a check command checks that an assertion is implied by the conjunction of all declared facts. If your facts are inconsistent, in the sense that their conjunction is false, or admit only very trivial instances (for example empty ones), your assertion can be trivially true. For example, in this example we changed one of the facts before our final check that yielded no counter-examples. We should have checked that this change did not accidentally make our specification inconsistent. To do so we could execute a run command after the final check, and iterate a bit through the returned instances to make sure the specification is still consistent and admits non-trivial file systems. Of course, just pressing New is not the ideal method to check if expected file system examples are still possible. In section Defining test scenarios with formulas we will see how to define run commands that behave like unit tests that directly search for specific instances of a specification.

So far we used only a reduced subset of all relational logic operators that are part of Alloy’s syntax. We did use the two most important ones, composition (.) and transitive closure (^), and with these alone (plus the standard set theory operators) it is possible to write most facts and assertions of interest. For a complete list of relational logic operators please see the A relational logic primer chapter.

Using higher-arity relations

Caution

This chapter is still under construction

abstract sig Object {}

sig File extends Object {}

sig Dir extends Object {
  contents : Name -> Object
}

one sig Root extends Dir {}

sig Name {}

fact {
  // Different entries in the same directory must have different names
  all d : Dir, n : Name | lone n.(d.contents)
}

fact {
  // A directory cannot be contained in more than one directory
  all o : Dir | lone contents.o
}

fact {
  // Directories cannot contain themselves directly or indirectly
  all d : Dir | d not in d.^{ d : Dir, o : Object | some d.contents.o }
}

fact {
  // Every object except the root is contained somewhere
  Name.(Object.contents) = Object - Root
}

Exercises

1. To practice relational logic, access the following Alloy4Fun models and specify all the listed constraints. Each constraint is specified in a separate predicate, and for each there is a command that can be used to check its correctness. If the constraint is not correctly specified a counter-example will be shown. The counter-example will include an atom that clarifies if it is an example that the incorrect constraint is currently rejecting but should be accepted or one that is currently being accepted but should be rejected.

   1. Photo sharing social network

   2. Graphs

   3. Production line

   4. Train station

   5. Courses

2. Specify the Git Object Model using Alloy. Focus on the connection between the different kinds of objects and ignore details like authors or committers. Start with a version that abstracts away the hashes that identify the objects and connect them directly instead. In a second version add the explicit hashes and the constraints that characterize them. Try to customize the visualizer theme to simplify to comprehension of instances. In particular, in the second version with explicit hashes, try to define auxiliary relations that can be used in the visualizer to depict the connections between the objects.

3. Specify Red-Black Trees using Alloy. To specify the constraint that “every path from a given node to any of its descendant NIL nodes goes through the same number of black nodes” you can use the cardinality operator (#), but be careful with the scope of Int (the scope sets the desired bit-width). Try to customize the visualizer theme to simplify to comprehension of instances.