A relational logic primer

In Alloy, constraints are specified in relational logic, an extension of first-order logic with a few operators to compose relations. In this chapter we will present this logic in detail, namely detail the semantics of each of the operators, illustrated with several usage examples. These examples will be based on the file system specification introduced in chapter Structural design with Alloy, whose signatures and fields are detailed below.

abstract sig Object {}

sig File extends Object {}

sig Dir extends Object {
  entries : set Entry
}

one sig Root extends Dir {}

sig Entry {
  name : one Name,
  object : one Object
}

sig Name {}

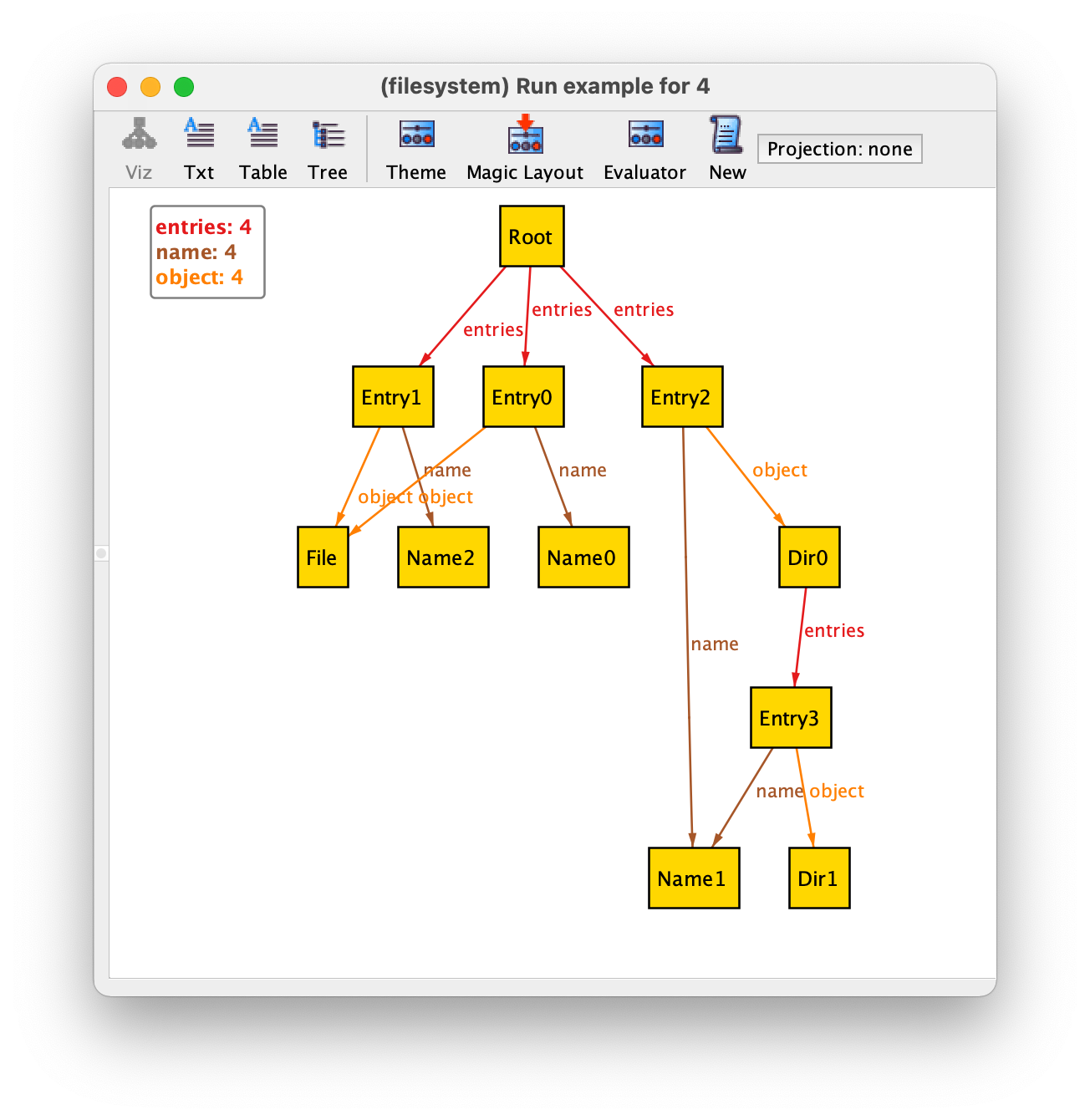
We will also use the following instance of this specification to illustrate the result of relational operators.

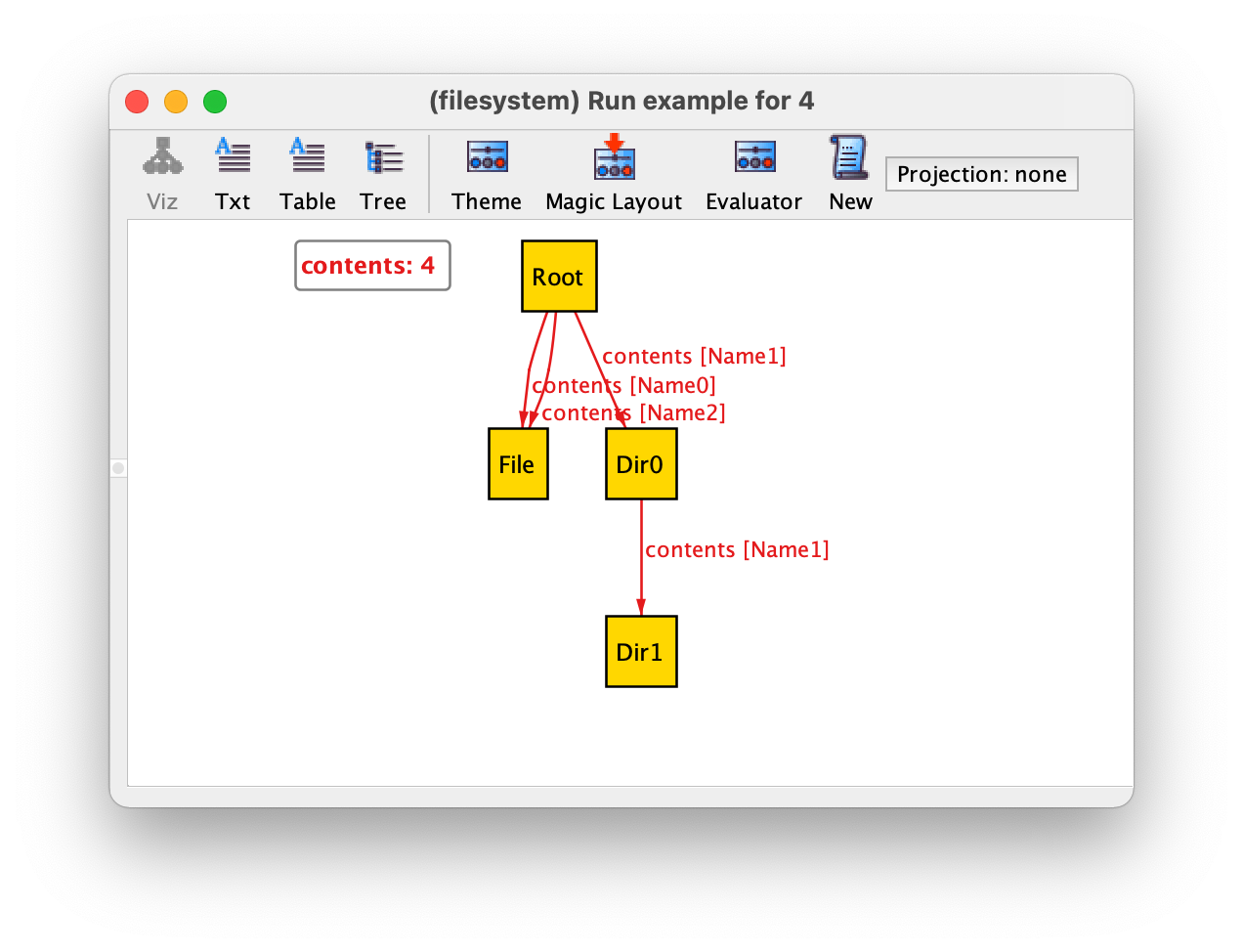
Occasionally we will also refer to the ternary relation contents used in the alternative version presented in Using higher-arity relations, whose content for the same instance of a file system is depicted below.

Everything is a relation

Structures are described in Alloy using only (mathematical) relations. A relation is a set of tuples of objects drawn from the universe of discourse. Every tuple in a relation must have the same size, which is known as the arity of the relation.

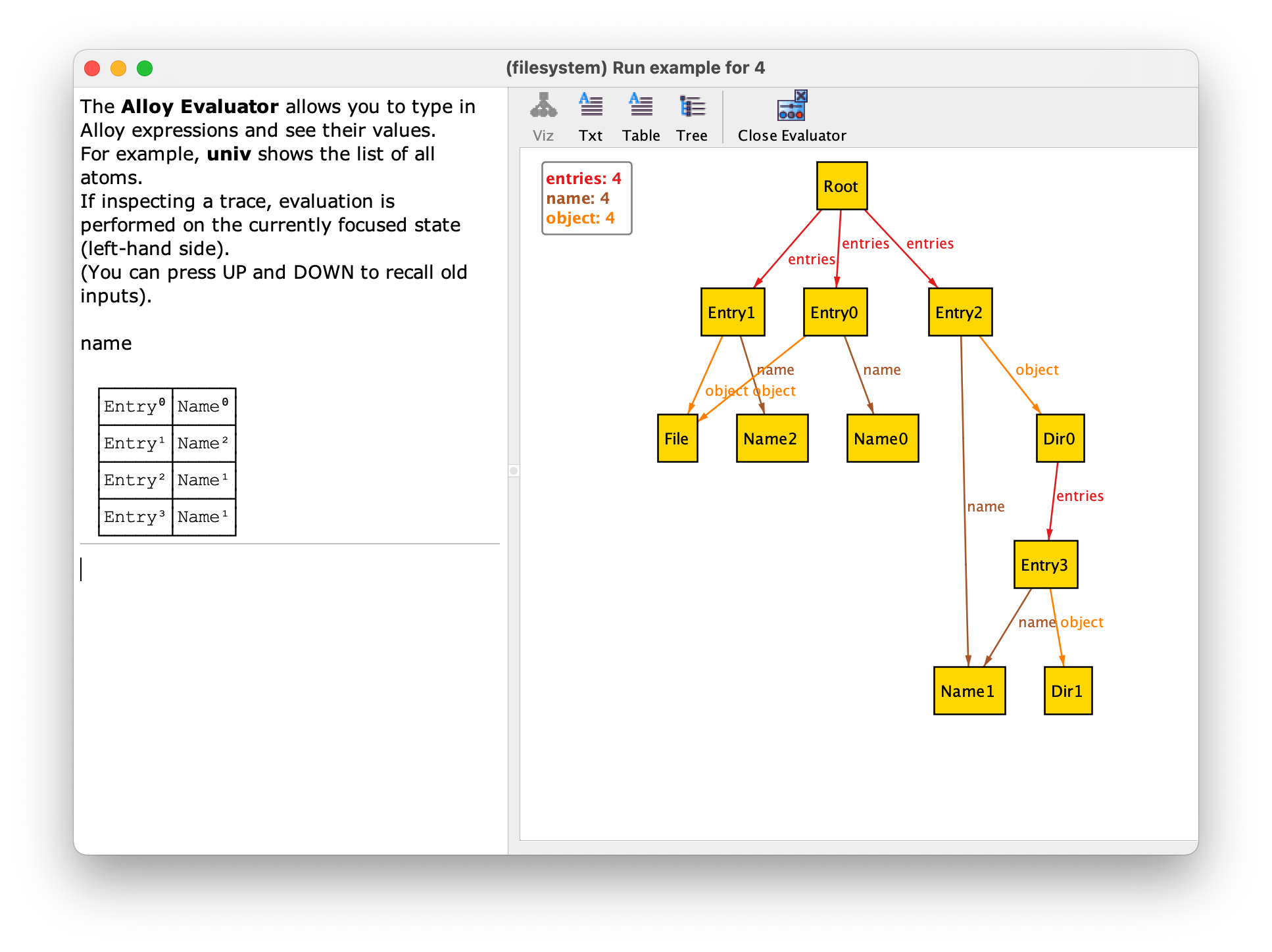
For example, field name is a relation of arity 2 (a binary relation) relating entries with their names. For the above instance, it has four pairs, namely:

name = {(Entry0,Name0),(Entry1,Name2),(Entry2,Name1),(Entry3,Name1)}

In logic a relation is also known as a predicate, and the fact that predicate name holds for tuple (x,y) is usually denoted as name(x,y). As explained later, in Alloy this fact can be denoted by x->y in name.

An alternative way to depict a relation (or predicate) is using a table, where each row corresponds to one of the tuples of the relation. The table view of relation name is depicted below.

`Entry0`	`Name0`
`Entry1`	`Name2`
`Entry2`	`Name1`
`Entry3`	`Name1`

This is also the standard way to present the value of relations in the Alloy Analyzer’s evaluator.

Relation contents is a relation of arity 3 (a ternary relation), relating directories, names, and objects. It contains four triples, namely:

contents = {(Root,Name1,Dir0),(Root,Name0,File),(Root,Name2,File),(Dir0,Name1,Dir1)}

A set can also be represented by a relation of arity 1. In Alloy, signatures are encoded in this way. For example, in the above instance, signature Dir has the value:

Dir = {(Root),(Dir0),(Dir1)}

Moreover, in Alloy even the constants and (quantified) variables are represented by relations, namely singleton relations of arity 1. A singleton is a relation with a single tuple. For example, signature Root, declared with multiplicity one, has the following value.

Root = {(Root)}

Warning

Singleton signature names vs atom names.

Do not confuse the two occurrences of the word Root in the above definition. On the left-hand side, we have the signature Root that was declared in our specification to denote the root of the file system. On the right-hand side, we have the atom Root of the universe, whose name was automatically generated by the Analyzer to populate signature Root. The name of this atom is actually irrelevant, but the Analyzer names atoms using the signature name as prefix and a sequential number as suffix. Actually, according to this naming convention, the name of this atom is Root0, and that is the name that will be depicted in the evaluator if you ask for the value of signature Root. However, in the visualiser, if there is only a single atom with a given name prefix the numeric suffix is omitted by default. In this chapter we will use the names chosen by the visualiser.

Since atom names are arbitrary, when specifying constraints in Alloy it is impossible to refer to them directly. If we need to distinguish a particular atom of the universe, we need to declare a singleton signature that will contain that atom and refer to that signature name instead. That was precisely what we did to distinguish the root of a file system.

An instance of an Alloy specification without mutable declarations is a single snapshot with a complete valuation for all declared signatures and fields, mapping each of them to a relation of the appropriate arity. The value of all signatures and fields in our example instance is the following.

Object   = {(Root),(Dir0),(Dir1),(File)}
Dir      = {(Root),(Dir0),(Dir1)}
Root     = {(Root)}
File     = {(File)}
Entry    = {(Entry0),(Entry1),(Entry2),(Entry3)}
Name     = {(Name0),(Name1),(Name2)}

entries  = {(Root,Entry0),(Root,Entry1),(Root,Entry2),(Dir0,Entry3)}
object   = {(Entry0,File),(Entry1,File),(Entry2,Dir0),(Entry3,Dir1)}
name     = {(Entry0,Name0),(Entry1,Name2),(Entry2,Name1),(Entry3,Name1)}
contents = {(Root,Name1,Dir0),(Root,Name0,File),(Root,Name2,File),(Dir0,Name1,Dir1)}

An instance also includes the values of the three predefined constants: none (the empty set), univ (the universe of all atoms), and iden (the identity relation on the universe). In our example instance their value is the following.

none = {}
univ = {(Root),(Dir0),(Dir1),(File),(Entry0),(Entry1),(Entry2),(Entry3),(Name0),(Name1),(Name2)}
iden = {(Root,Root),(Dir0,Dir0),(Dir1,Dir1),(File,File),(Entry0,Entry0),(Entry1,Entry1),(Entry2,Entry2),(Entry3,Entry3),(Name0,Name0),(Name1,Name1),(Name2,Name2)}

First-order logic in a nutshell

Relational logic is an extension of first-order logic, which in turn is an extension of propositional logic. In propositional logic the simplest (atomic) formula is a proposition that checks if a Boolean variable is true. Compound formulas can be built by connecting atomic formulas using the standard logic connectives (or operators): negation, conjunction, disjunction, implication, and equivalence. These connectives are also available in Alloy’s relational logic, and their syntax is the following.

Operator	Name
`!`, `not`	Negation
`&&`, `and`	Conjunction
`\|\|`, `or`	Disjunction
`=>`, `implies`	Implication
`<=>`, `iff`	Equivalence

As you can see, Alloy has a dual syntax for these operators, one with programming language style symbols and the other with English words. In this book we tend to use the latter, as the resulting formulas are more readable. The implies operator can also have an optional else to state what should be true when the condition on the left-hand side is false. Given arbitrary formulas P, Q, T, P implies Q else T is the same as (P and Q) or (not P and T).

In first-order logic we have a domain of discourse (or universe), and propositions are generalised by predicates that relate elements of this domain. Formulas can also be built using variables quantified over this domain. There are two standard quantifiers: the universal quantifier ∀ x . P checks if a formula P (possibly referring to variable x) is true for all x in the domain; and the existential quantifier ∃ x . P checks if a formula P (possibly referring to variable x) is true for some x in the domain. In Alloy all quantifications are bounded by a set, and English words are used instead of the standard mathematical notation. The following table presents all quantifiers that are available in Alloy: A is denotes an arbitrary set (a unary relation) and P an arbitrary formula. The first two are the standard universal and existential quantifiers.

Quantifier	Informal meaning
`all x : A \| P`	`P` is true for all `x` in set `A`
`some x : A \| P`	`P` is true for some `x` in set `A`
`no x : A \| P`	`P` is false for all `x` in set `A`
`lone x : A \| P`	`P` is true for at most one `x` in set `A`
`one x : A \| P`	`P` is true for exactly one `x` in set `A`

It is well known that the existential quantifier can be specified with the universal one, and vice-versa, and the same is true for all other Alloy quantifiers. For example, some x : A | P is the same as not (all x : A | not P) and no x : A | P is the same as all x : A | not P.

As mentioned above in Alloy everything is a relation. The same is true for quantified variables: the quantified x that can be referred in P is a unary relation containing a single tuple with an atom of the universe. It is also possible to quantify more than one variable at once, as in all x,y : A | P or all x : A, y : B | P. In the latter, the expression B can also refer to the first quantified variable x. It is also possible to add keyword disj to quantify over all different values of the bound variables. For example, writing all disj x,y : A | P abbreviates all x,y : A | x != y implies P.

Besides predicates, first-order logic also allows functions as non-logical symbols. Given some parameters a function returns an element of the domain. Since in Alloy the atoms of the universe are mostly uninterpreted there are very few predefined functions. The exception is when using integers, for which we have the standard arithmetic operations. If we do not consider functions, atomic formulas in first-order logic just check for equality of (quantified) variables or if a tuple of (quantified) variables satisfies (or is a member of) a predicate. In Alloy’s relational logic we have a few more atomic formulas, that are described in the following table, where R and S are arbitrary relations of the same arity, including sets.

Atomic formula	Informal meaning
`R in S`	`R` is a subset or equal to `S`
`R = S`	`R` is equal to `S`
`some R`	`R` contains at least one tuple
`lone R`	`R` contains at most one tuple
`one R`	`R` contains exactly one tuple
`no R`	`R` is empty

The negation of the subset or equality atomic formulas can also be written by placing the negation operator next to the comparison operator. For example, instead of not (R in S) it is possible to write R not in S or R !in S.

Since quantified variables are also (singleton) relations, although in stands for the subset or equal operator (\(⊆\)) it can also be used to check set membership (∈). As we will see below, given variables x₁, …, xₐ, it is possible to define expression x₁->…->xₐ that denotes a relation with a single tuple with those variables. Formula x₁->…->xₐ in R can then be used to check that this tuple belongs to a relation R with arity a, something that in the standard mathematical notation of first-order logic is written as R(x₁,…,xₐ). Recall that, besides equality checks between variables, such membership checks are the only atomic formulas in first-order logic. Although Alloy also allows all the above ones, they all can be written using just these basic checks, so technically they do not add expressive power to first-order logic, but just a more succinct way to write formulas. The following table provides such formal definitions, assuming R and S have arity a.

Atomic formula	Formal meaning
`R in S`	`all x₁,…,xₐ : univ \| x₁->…->xₐ in R implies x₁->…->xₐ in S`
`R = S`	`R in S and S in R`
`some R`	`some x₁,…,xₐ : univ \| x₁->…->xₐ in R`
`lone R`	`all x₁,…,xₐ,y₁,…,yₐ : univ \| x₁->…->xₐ in R and y₁->…->yₐ in R implies x₁=y₁ and … and xₐ=yₐ`
`one R`	`some R and lone R`
`no R`	`not (some R)`

As we can see, the reduction in formula size can be substantial. For example, to formalize the requirement that “every file is an object”, in plain first-order logic we would have to write ∀ x . File(x) → Object(x) or, in Alloy’s notation, all x : univ | x in File implies x in Object. However, with Alloy’s relational logic we can just write File in Object.

Warning

Be careful with membership checks!

It is important to always recall that in denotes the subset operator and not the membership test. Of course, if we are certain that the expression on the left-hand side is a singleton (a set with a single tuple), in behaves like membership. For example, to test that Root is a Dir we can write Root in Dir. However, if the expression on the left-hand side does not necessarily denote a singleton, this check may not work as expected. For example, if Root was declared with multiplicity lone instead of one, the check Root in Dir will also be true if Root is empty. In this case, to be certain to test for membership you also need to check that the left-hand expression is non-empty, as follows.

some Root and Root in Dir

Relational operators

As all the alternative atomic checks, most of the relational operators in Alloy do not technically add expressive power to first-order logic, but just a more succinct alternative to write formulas. The full list of operators is presented below.

Operator	Name
`+`	Union
`&`	Intersection
`-`	Difference
`.`	Composition, Dot join
`[]`	Box join
`->`	(Cartesian) Product
`<:`	Domain restriction
`:>`	Range restriction
`++`	Override
`~`	Transpose, Converse
`^`	Transitive closure
`*`	Reflexive transitive closure

These operators act like combinators, that can be used to put together relations (predicates) to obtain expressions denoting more complex relations. The most basic operators are the standard set operators of union, intersection, and difference. For example, given predicates File and Dir we can compose them with union to obtain the derived predicate File + Dir that can be used to directly check if an element is either a file or a directory. This simplifies the writing of requirements such as “every object is either a file or a directory”. In plain first-order logic we would write (using Alloy’s syntax):

all x : univ | x in Object implies x in File or x in Dir

By using the union operator we can simplify this to:

all x : univ | x in Object implies x in File + Dir

And finally by using the subset operator we can write just:

Object in File + Dir

Below we present the formal semantics of all relational operators in terms of plain first-order logic. The formula in the right column formally specifies when a tuple belongs to an expression that uses each operator. To abbreviate, in this formula all variables are implicitly universally quantified over the universe. Notice that some of these operators (namely the transpose and the closure operators) are only defined for binary relations.

Operator	Formal meaning
`+`	`x₁->…->xₐ in R+S iff x₁->…->xₐ in R or x₁->…->xₐ in S`
`&`	`x₁->…->xₐ in R&S iff x₁->…->xₐ in R and x₁->…->xₐ in S`
`-`	`x₁->…->xₐ in R-S iff x₁->…->xₐ in R and x₁->…->xₐ !in S`
`.`	`x₁->…->xₐ₋₁->y₂->…->yₑ in R.S iff x₁->…->xₐ in R and y₁->…->yₑ in S and xₐ = y₁`
`[]`	`x₁->…->xₐ in R[S] iff x₁->…->xₐ in S.R`
`->`	`x₁->…->xₐ->y₁->…->yₑ in R->S iff x₁->…->xₐ in R and y₁->…->yₑ in S`
`<:`	`x₁->…->xₐ in A<:R iff x₁ in A and x₁->…->xₐ in R`
`:>`	`x₁->…->xₐ in R:>A iff x₁->…->xₐ in R and xₐ in A`
`++`	`x₁->…->xₐ in R++S iff x₁->…->xₐ in S or (x₁->…->xₐ in R and x₁->y₂->…->yₐ !in S)`
`~`	`x₁->x₂ in ~R iff x₂->x₁ in R`
`^`	`x₁->x₂ in ^R iff x₁->x₂ in R + R.R + R.R.R + …`
`*`	`x₁->x₂ in *R iff x₁->x₂ in ^R + iden`

In the remainder of this section we will illustrate each operator with examples based on the file system specification presented above.

Composition

The entries inside the root

Root.entries
= {(Root)}.{(Root,Entry0),(Root,Entry1),(Root,Entry2),(Dir0,Entry3)}
= {(Entry0),(Entry1),(Entry2)}

The names of the entries inside the root

Root.entries.name
= {(Entry0),(Entry1),(Entry2)}.name
= {(Entry0),(Entry1),(Entry2)}.{(Entry0,Name0),(Entry1,Name2),(Entry2,Name1),(Entry3,Name1)}
= {(Name0),(Name2),(Name1)}

The binary relation between directories and the contained objects

entries.object
= {(Root,Entry0),(Root,Entry1),(Root,Entry2),(Dir0,Entry3)}.{(Entry0,File),(Entry1,File),(Entry2,Dir0),(Entry3,Dir1)}
= {(Root,File),(Root,Dir0),(Dir0,Dir1)}

Non-empty directories

entries.Entry
= {(Root,Entry0),(Root,Entry1),(Root,Entry2),(Dir0,Entry3)}.{(Entry0),(Entry1),(Entry2),(Entry3)}
= {(Root),(Dir0)}

(contents.Object).Name
= ({(Root,Name1,Dir0),(Root,Name0,File),(Root,Name2,File),(Dir0,Name1,Dir1)}.{(Root),(Dir0),(Dir1),(File)}).Name
= {(Root,Name1),(Root,Name0),(Root,Name2),(Dir0,Name1)}.Name
= {(Root,Name1),(Root,Name0),(Root,Name2),(Dir0,Name1)}.{(Name0),(Name1),(Name2)}
= {(Root),(Dir0)}

Set operators

All directories except the root

Dir - Root
= {(Root),(Dir0),(Dir1)} - {(Root)}
= {(Dir0),(Dir1)}

The directories inside the root

Root.entries.object & Dir
= Root.{(Root,File),(Root,Dir0),(Dir0,Dir1)} & Dir
= {(File),(Dir0)} & {(Root),(Dir0),(Dir1)}
= {(Dir0)}

Cartesian product

All possible associations between files and names

File->Name
= {(File)} -> {(Name0),(Name1),(Name3)}
= {(File,Name0),(File,Name1),(File,Name3)}

Domain and range restriction

The identity relation on objects

Object <: iden
= {(Root),(Dir0),(Dir1),(File)} <: {(Root,Root),(Dir0,Dir0),(Dir1,Dir1),(File,File),(Entry0,Entry0),(Entry1,Entry1),(Entry2,Entry2),(Entry3,Entry3),(Name0,Name0),(Name1,Name1),(Name2,Name2)}
= {(Root,Root),(Dir0,Dir0),(Dir1,Dir1),(File,File)}

Override

A modified entries relation where all files are removed from the root directory

entries ++ (Root -> (Root.entries & object.Dir))
= entries ++ (Root -> ({(Root)}.{(Root,Entry0),(Root,Entry1),(Root,Entry2),(Dir0,Entry3)} & object.Dir))
= entries ++ (Root -> ({(Entry0),(Entry1),(Entry2)} & object.Dir))
= entries ++ (Root -> ({(Entry0),(Entry1),(Entry2)} & {(Entry0,File),(Entry1,File),(Entry2,Dir0),(Entry3,Dir1)}.{(Root),(Dir0),(Dir1)}))
= entries ++ (Root -> ({(Entry0),(Entry1),(Entry2)} & {(Entry2),(Entry3)}))
= entries ++ (Root -> {(Entry2)})
= entries ++ ({(Root)} -> {(Entry2)})
= entries ++ ({(Root,Entry2)})
= {(Root,Entry0),(Root,Entry1),(Root,Entry2),(Dir0,Entry3)} ++ ({(Root,Entry2)})
= {(Root,Entry2),(Dir0,Entry3)}

Transpose

The binary relation between objects (contained in directories) and their name

~object.name
= ~{(Entry0,File),(Entry1,File),(Entry2,Dir0),(Entry3,Dir1)}.{(Entry0,Name0),(Entry1,Name2),(Entry2,Name1),(Entry3,Name1)}
= {(File,Entry0),(File,Entry1),(Dir0,Entry2),(Dir1,Entry3)}.{(Entry0,Name0),(Entry1,Name2),(Entry2,Name1),(Entry3,Name1)}
= {(File,Name0),(File,Name2),(Dir0,Name1),(Dir1,Name1)}

~(Object.contents)
= ~({(Root),(Dir0),(Dir1),(File)}.{(Root,Name1,Dir0),(Root,Name0,File),(Root,Name2,File),(Dir0,Name1,Dir1)})
= ~{(Name1,Dir0),(Name0,File),(Name2,File),(Name1,Dir1)}
= {(File,Name0),(File,Name2),(Dir0,Name1),(Dir1,Name1)}

The binary relation between entries in the same directory

~entries.entries
= ~{(Root,Entry0),(Root,Entry1),(Root,Entry2),(Dir0,Entry3)}.{(Root,Entry0),(Root,Entry1),(Root,Entry2),(Dir0,Entry3)}
= {(Entry0,Root),(Entry1,Root),(Entry2,Root),(Entry3,Dir0)}.{(Root,Entry0),(Root,Entry1),(Root,Entry2),(Dir0,Entry3)}
= {(Entry0,Entry0),(Entry0,Entry1),(Entry0,Entry2),(Entry1,Entry0),(Entry1,Entry1),(Entry1,Entry2),(Entry2,Entry0),(Entry2,Entry1),(Entry2,Entry2),(Entry3,Entry3)}

The binary relation between entries sharing names

name.~name
= {(Entry0,Name0),(Entry1,Name2),(Entry2,Name1),(Entry3,Name1)}.~{(Entry0,Name0),(Entry1,Name2),(Entry2,Name1),(Entry3,Name1)}
= {(Entry0,Name0),(Entry1,Name2),(Entry2,Name1),(Entry3,Name1)}.{(Name0,Entry0),(Name2,Entry1),(Name1,Entry2),(Name1,Entry3)}
= {(Entry0,Entry0),(Entry1,Entry1),(Entry2,Entry2),(Entry2,Entry3),(Entry3,Entry2),(Entry3,Entry3)}

Closures

The binary relation between a directory and the objects contained in that directory or any sub-directory

^(entries.object)
= ^{(Root,File),(Root,Dir0),(Dir0,Dir1)}
= {(Root,File),(Root,Dir0),(Root,Dir1),(Dir0,Dir1)}

All objects in the file system

Root.*(entries.object)
= Root.(^(entries.object) + iden)
= Root.({(Root,File),(Root,Dir0),(Root,Dir1),(Dir0,Dir1)} + iden)
= {(Root)}.{(Root,File),(Root,Dir0),(Root,Dir1),(Dir0,Dir1),(Root,Root),(Dir0,Dir0),(Dir1,Dir1),(File,File),(Entry0,Entry0),(Entry1,Entry1),(Entry2,Entry2),(Entry3,Entry3),(Name0,Name0),(Name1,Name1),(Name2,Name2)}
= {(Root),(Dir0),(Dir1),(File)}

Set comprehension

The binary relation between directories and the contained objects

{ d : Dir, o : Object | some d.contents.o }
= {(Root,File),(Root,Dir0),(Dir0,Dir1)}

Note

A question of style!

An object is not contained in more one entry, or relation content is injective.

The pure first-order (or point-wise) style.

all x,y : Entry, o : Object | x->o in object and y->o in object implies x=y

The most common Alloy navigational style.

all o : Object | lone object.o

The pure relational (or point-free) style.

object.~object in iden

A type-system for relational specifications

Caution

This section is still under construction