MFP

Índice
| Métodos Formais em Engenharia de Software |
|---|
| Cálculo de Sistemas de Informação |
| Programação Ciber-física |
| Verificação Formal |
| Projecto em MFP |
| Anos anteriores |
| Calendário | Sumários |
| Alumni |
Introdução ao Assistente de Prova Coq
Ferramentas de prova automática baseadas na noção semântica de satisfatibilidade, como é o caso dos SAT solvers e SMT solvers, funcionam procurando um modelo para uma fórmula. As ferramentas baseadas nesta abordagem não são mais do que procedimentos de decisão que produzem uma resposta “SAT/UNSAT/UNKNOWN”. Para testar a validade de uma fórmula $\phi$ usando estas ferramentas, introduzimos a sua negação $\neg \phi$ e se obtivermos como resposta SAT ficamos a saber que a fórmula não é válida (pois foi encontrado um modelo para a sua negação). Se a resposta for UNSAT temos a garantia que a fórmula $\phi$ é válida (pois não há nenhum modelo para a sua negação), mas não é dada nenhuma justificação. Se a fórmula $\phi$ for “complexa” haverá uma forte probabilidade de a resposta ser UNKNOWN.
Há um outro grupo de ferramentas de prova que seguem uma abordagem alternativa à lógica, chamada “dedutiva”, que é focada na relação de dedução induzida nas fórmulas por um sistema de regras de inferência (sistema de prova). Estas ferramentas têm por objectivo provar a validade de uma fórmula com base nessas regras, construindo uma derivação (árvore de prova) que justifica a sua validade. Neste processo é usual o utilizador conduzir a prova (embora possa utilizar muitas estratégias automáticas), pelo que este tipo de ferramentas costumam ser chamadas de Interactive Theorem Provers ou Proof Assistants.
Num assistente de prova, o utilizador, após formalizar as noções primitivas da teoria (em estudo), desenvolve as provas interativamente (por meio de táticas de prova), e quando uma prova é finalizada um termo (ou script) de prova é criado. A utilização destas ferramentas tem-se popularizado muito e, embora acarrete um custo inicial de aprendizagem de utilização, mostra-se muito vantajosa nos seguintes aspectos: ajuda a lidar com problemas de grande dimensão; impede que se descurem detalhes; permite o arquivamento das provas e a reutilização de resultados já provados.
A idoneidade de um assistente de prova é naturalmente uma característica essencial, para qual contribui chamado o Critério de Bruijn: “os objectos de prova gerados devem poder ser verificados por um algoritmo simples”. Vamos estudar um assistente de prova que segue este critério — o sistema Coq.
O Coq é um assistente de prova que está em desenvolvimento contínuo há mais de 30 anos, e que recebeu o prémio ACM Software System em 2013. Tem sido usado em vários projetos de verificação emblemáticos (de que são exemplos o compilador de C certificado CompCert e o projecto Verified Software Toolchain para verificação de programas C) e serviu para a formalização do teorema das quatro cores (entre muitas outras formalizações matemáticas).
O Coq é baseado num formalismo que é, simultameamente, uma lógica muito expressiva e uma linguagem de programação ricamente tipificada – o Cálculo de Construções Indutivas. O seu funcionamento tem por base a correspondência “proposições-como-tipos” e “provas-como-programas”, numa lógica de ordem superior intuicionista.
Antes de nos focarmos no sistema Coq vamos fazer uma breve apresentação de alguns tópicos importantes para a sua compreensão.
Dedução Natural
A dedução natural é uma formalização do raciocínio matemático, introduzida por Gerhard Gentzen na primeira metade do século XX como uma representação “natural” de derivações lógicas. O sistema de prova é constituído por um conjunto de regras. Para cada conectiva lógica existem “regras de introdução” (onde a conectiva aparece na conclusão da regra) e “regras de eliminação” (onde a conectiva aparece nas premissas da regra. Vamos apresentar aqui o conjunto de regras de dedução natural para a lógica de primeira ordem clássica, usando sequentes.
- Um sequente é um juízo da forma $\Gamma \vdash \phi$, onde $\Gamma$ é um conjunto de fórmulas (o contexto) e $\phi$ uma fórmula (a conclusão do sequente).
- O juízo $\Gamma \vdash \phi$ deve ler-se: “ $\phi$ pode ser deduzida do conjunto de hipóteses $\Gamma$”, ou “ $\phi$ é uma consequência de $\Gamma$”.
O uso de sequentes permite uma representação clara do cancelamento de hipóteses, e o Coq usa sequentes na apresentação do estado da prova.
As regras para as conectivas proposicionais são as seguintes:

|
Exemplo de uma árvore de prova desenvolvida em retrocesso, em forma de tabela:

As provas desenvolvidas num assistente de prova são também em retrocesso. Seguem o método conhecido como “goal directed proof”:
- O utilizador insere a fórmula que deseja provar.
- O sistema exibe a fórmula a ser provada, com o contexto de factos locais que podem ser usados para esta prova.
- O utilizador insere um comando (uma regra básica ou uma tática) para decompor o objetivo de prova em objetivos mais simples.
- O sistema exibe a lista de fórmulas que ainda precisam ser provadas.
- Quando não restarem mais fórmulas para provar, prova está completa e poderá ser guardada.
As regras para os quantificadores têm condições laterais que têm que ser satisfeitas. Estas podem ser descritas utilizando a operação sintática de substituição:
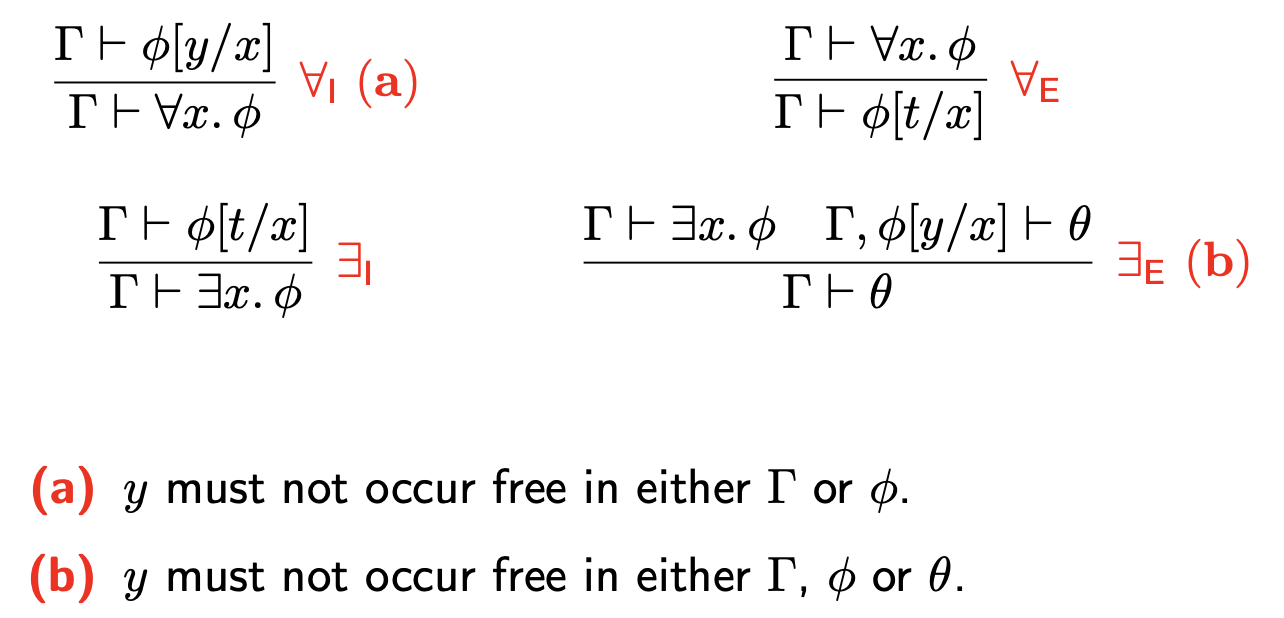
|
Exemplo de uma árvore de prova (repare que quando a regra de $\exists_E$ é aplicada, uma nova variável $x_0$ é introduzida):

A prova por redução ao absurdo está codificada na regra RAA (reductio ad absurdum) e é o que dá a esta lógica uma caracter “clássico”. Com ela podemos, por exemplo, provar o “princípio do meio excluído”.

Porém, há um ramo da lógica que rejeita este princípio.
Lógica Clássica vs Lógica Intuicionista
A compreensão clássica da lógica é baseada na noção de verdade. A verdade de uma afirmação é “absoluta” e independente de qualquer raciocínio. Portanto, as afirmações são verdadeiras ou falsas, e a proposição $(A \vee \neg A)$ deve ser válida independentemente do significado de $A$.
A lógica intuicionista (ou construtiva) é um ramo da lógica formal que rejeita este princípio orientador. Baseia-se na noção de prova. O julgamento sobre uma afirmação baseia-se na existência de uma prova (ou “construção”) dessa afirmação. Para que $(A \vee \neg A)$ seja válida é necessário ter uma prova de $A$ ou uma prova de $\neg A$ (mostrando que assumir uma prova de $A$ conduz a uma contradição).
Provas por redução ao absurdo, ou usando a lei do meio excluído, não são construtivas/intuicionistas. Mas, se retirarmos a regra RAA ao sistema de prova acima apresentado, o sistema deixa de ser clássico e passa a ser intuicionista.
Tudo o que se prova no sistema intuicionista também se prova na lógica clássica. Contudo, e como era de esperar, há algumas tautologias da lógica clássica que não são válidas na lógica intuicionista. Por exemplo,

Tradicionalmente, a lógica clássica é definida pela extensão da lógica intuicionista com uma das seguintes leis: lei de redução ao absurdo, lei da dupla negação, lei do meio excluído ou lei de Pierce.
Proposições como Tipos
A interpretação das “proposições como tipos” estabelece uma relação precisa entre a lógica intuicionista e o lambda calculus:
- uma proposição $A$ é vista como um tipo (o tipo das suas provas);
- uma prova de $A$ é vista como um termo do tipo $A$.
Portanto, uma proposição $A$ é demonstrável apenas no caso do tipo $A$ ser habitado, e o mecanismo de type checking pode ser usado para verificar uma prova.

A decidibilidade do type checking está, portanto, no cerne dos assistentes de prova fundamentados nestes princípios, como é o caso do Coq. No final do desenvolvimento de uma prova, o termo de prova é verificado quanto ao tipo e o tipo é comparado com o objetivo de prova original. É esta característica faz com que o Coq cumpra o Critério de Bruijn, uma vez que o algoritmo de type checking é simples e robusto.
Esta analogia entre lógica formal e cálculo computacional foi estabelecida por Haskell Curry e William Howard. O isomorfismo de Curry-Howard estabelece uma correspondência entre a dedução natural para a lógica intuicionista e o lambda calculus.
Lambda Calculus
O lambda calculus (introduzido na década de 1930 por Alonzo Church) é um sistema formal para expressar computação, baseado na construção de funções (pelo mecanismo de abstração) e na aplicação de funções (pelo mecanismo de substituição de variáveis). O lambda calculus tipificado introduz uma disciplina de tipos sobre os termos. Os tipos são entidades de natureza sintática associadas aos lambda termos. A natureza concreta dos tipos depende do cálculo lambda em causa. Estes calculi estão na base das linguagens funcionais de programação e da teoria da prova via o isomorfismo das “proposições como tipos”.
Na sua versão mais simples, $\lambda_\rightarrow$, a sintaxe do lambda calculus tipificado é a seguinte:

O termo $(\lambda x:\tau . e)$ representa a função de parâmetro $x$, de tipo $\tau$, e corpo $e$, e o termo $(a b)$ denota a aplicação da função $a$ ao argumento $b$.
Para evitar a proliferação de parêntesis, são usadas as seguintes convenções:
- a construção de tipo $\to$ é associativa à direita;
- a aplicação é associativa à esquerda;
- o alcance da abstração $\lambda$ estende-se para a direita tanto quanto possível.
No sistema de tipos deste calculus, as funções são classificadas com tipos simples que determinam o tipo de seus argumentos e o tipo dos valores que produzem, e podem ser aplicadas apenas a argumentos do tipo apropriado. Para descrever as regras de tipo é necessária uma noção de contexto para declarar as variáveis livres (isto é, que não estão a ser abstraidas por um $\lambda$). Neste caso, um contexto é um conjunto $\Gamma$ de declarações de variáveis e usamos a seguinte sintaxe: $\quad \Gamma ::= \quad . | \Gamma, x : \tau$
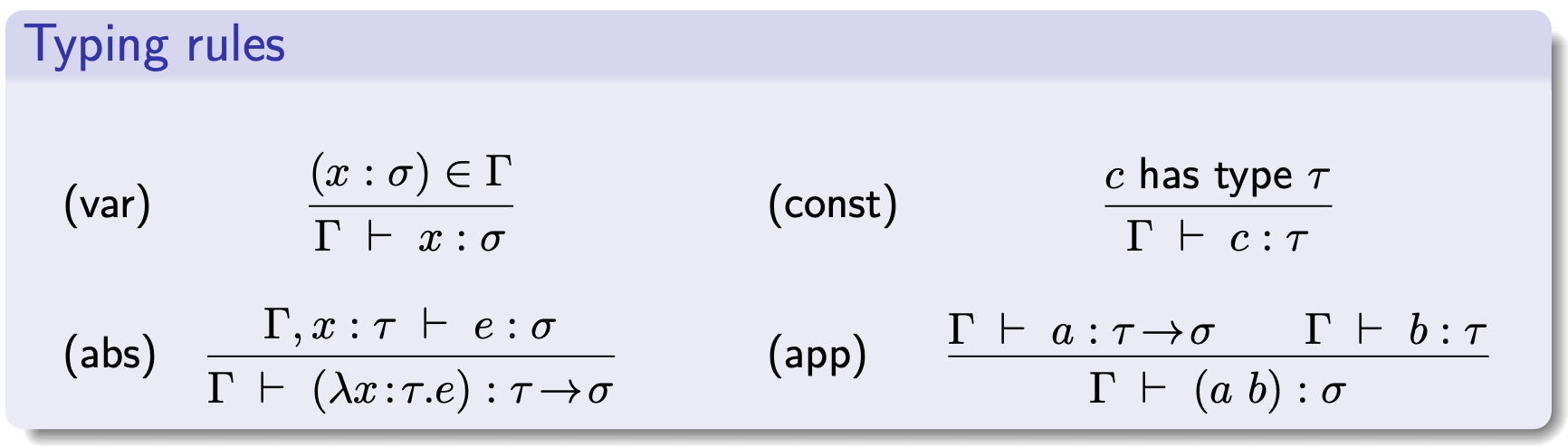
Um termo $a$ diz-se “bem tipificado” (ou “bem tipado”) se existirem $\Gamma$ e $\sigma$ tal que $\Gamma \vdash a : \sigma$.
Aqui está um exemplo de uma árvore derivação para um juízo de tipo.

Num termo, uma variável que está abstraída por um $\lambda$ diz-se ligada, caso contrário diz-se livre. $\mathsf{FV}(e)$ denota o conjunto das variáveis livres do termo $e$. Por exemplo, em $(\lambda x: \tau. y x)$, a variável $x$ é ligada e a $y$ é livre. Naturalmente que o nome das variáveis ligadas não é importante, e podemos renomea-las com novos nomes (conversão- $\alpha$), desde que não colidam com nomes de variáveis livres em uso. Por exemplo: $(\lambda x: \tau. y x) =(\lambda z: \tau. y z)$.
Os termos são manipulados por uma regra de computação ($\beta$-redução) que indica como calcular o valor de uma função para um dado argumento, e que se baseia na noção de substituição. Na aplicação de uma substituição a um termo, contamos com a convenção das variáveis: “todas as variáveis ligadas são escolhidas para serem diferentes das variáveis livres”. Assim, a acção de uma substituição num termo é definida com possíveis renomeações das variáveis ligadas.

Geralmente há mais do que uma maneira de realizar cálculos.
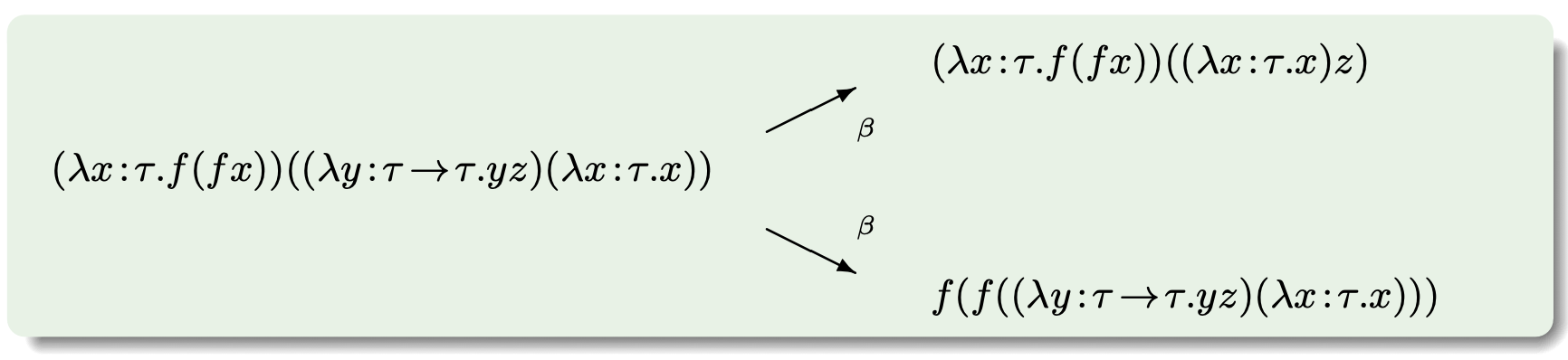
Um termo diz-se uma forma normal se não contém redexes, e diz-se fortemente normalizável se qualquer sequência de redução conduzir sempre a uma forma normal. As estratégias usuais de redução são call-by-name (selecionar o redex mais à esquerda e mais externo) e call-by-value (selecionar o redex mais à esquerda e mais interno).
Propriedades deste sistema:
- Unicidade de tipos: $\quad$ Se $\Gamma \vdash a : \sigma$ e $\Gamma \vdash a : \tau$, então $\sigma = \tau$.
- Inferência de tipos: $\quad$ Pode-se deduzir automaticamente o tipo (se existir) de um termo num dado contexto.
- Preservação de tipos: $\quad$ Se $\Gamma \vdash a : \sigma$ e $a \rightarrow_\beta b$, então $\Gamma \vdash b : \sigma$.
- Normalização forte: $\quad$ Se $\Gamma \vdash a : \sigma$, então $a$ é fortemente normalizável.
- Confluência: $\quad$ Se $a \equiv_{\beta} b$, então $a \twoheadrightarrow_{\beta} e$ e $b \twoheadrightarrow_{\beta} e$, para algum termo $e$.
- Substituição: $\quad$ Se $\Gamma, x:\tau \vdash a : \sigma$ e $~\Gamma \vdash b:\tau$, então $\Gamma \vdash a[b/x] : \sigma$.
- Enfraquecimento: $\quad$ Se $\Gamma \vdash a : \sigma$ e $\Gamma\subseteq \Gamma’$, então $\Gamma’ \vdash a : \sigma$.
- Fortalecimento: $\quad$ Se $\Gamma, x:\tau \vdash a : \sigma$ e $x\not\in\mathsf{FV}(a)$, então $\Gamma \vdash a : \sigma$.
O Isomorfismo de Curry-Howard
O isomorfismo de Curry-Howard estabelece uma correspondência entre a dedução natural para a lógica intuicionista e o lambda calculus.

Este isomorfismo, apresentado aqui na sua versão mais simples, pode ser levado para o patamar mais elevado da lógica de ordem superior (onde é possível quantificar sobre funções e sobre predicados). Na apresentação destes lambda calculi, em vez de termos duas categorias distintas de expressões (termos e tipos), temos uma categoria única de expressões, que são chamadas de pseudo-termos.

|
Existe um conjunto de sorts (constantes que denotam os universos do sistema de tipos) organizadas hierarquicamente e regras de tipo que determinam que tipos de funções dependentes se podem construir e em que sort eles habitam.
O Sistema Coq
O Coq é um assistente de prova baseado no Calculus of Inductive Constructions (CIC), uma teoria de tipos ordem superior enriquecida com tipos indutivos. Os mecanismos de eliminação (recursores e princípios de indução) são gerados automaticamente a partir das definições indutivas. O sistema Coq está assente na correspondência “proposições-como-tipos” e “provas-como-programas”. A linguagem das provas é uma linguagem de programação. Trabalha com lógica intuicionista, onde uma prova é uma construção que produz testemunhas para declarações existenciais e provas efectivas para as disjunções, o que permite fazer extração de programas a partir da sua especificação.
No CIC todos os objetos possuem um tipo, e os tipos são classificados pelos sorts: Prop (proposições lógicas), Set (coleções matemáticas) e Type (tipos abstratos).
O sistema Coq é constituido por:
- uma linguagem de especificação — Gallina — que permite desenvolver teorias matemáticas e escrever especificações de programas.
- uma linguagem de comandos — Vernacular — que permite fazer pedidos ao sistema.
- uma linguagem domain-specific — Ltac — que permite desenvolver provas e táticas de prova.
Ilustramos a sintaxe da linguagem Gallina com estes pequenos exemplos:

O ambiente (lista de declarações e definições) em que as expressões são avaliadas e tipificadas é constituído por um ambiente global (eventualmente carregado de bibliotecas, e que vai sendo depois enriquecido pelo utilizador) e um contexto local.
O sistema Coq possui um mecanismo de blocos Section id. … End id. o que permite manipular o contexto local (expandindo-o e contraindo-o).
Vejamos um exemplo em que abrimos uma secção EX, declaramos localmente um conjunto A, um predicado P e uma proposição Q, e de seguida lançamos a prova de um lema e aplicamos táticas para o provar, criando um termo de prova. No final, com o comando Qed, o identificador example é definido com este termo de prova e adicionado ao contexto local.

Podemos ver o termo com o comando Print.

que corresponde ao seguinte lambda termo e juízo de tipo:
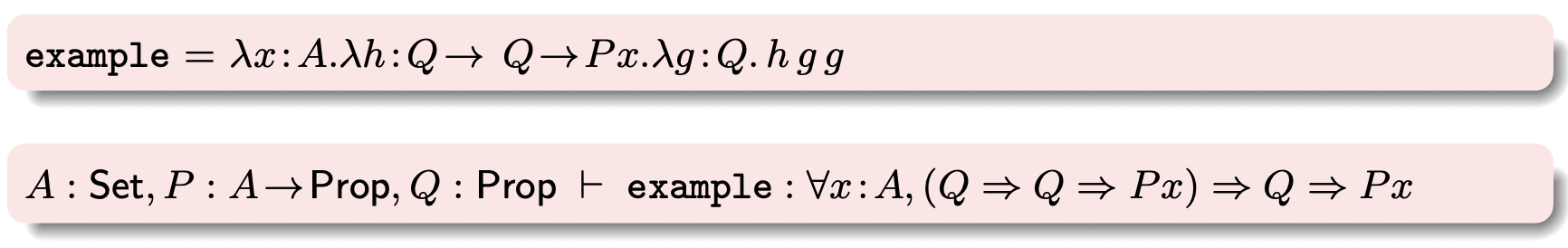
Ao fechar a secção EX as variáveis declaradas localmente na secção são abstraídas no termo de prova.

Táticas associadas às conectivas da lógica de primeira ordem.

|
Mais algumas táticas.

|
O CIC é uma teoria muito rica, com várias regras de redução que são aplicadas na avaliação do termos.

|
A avaliação de termos é feita com o comando Eval.
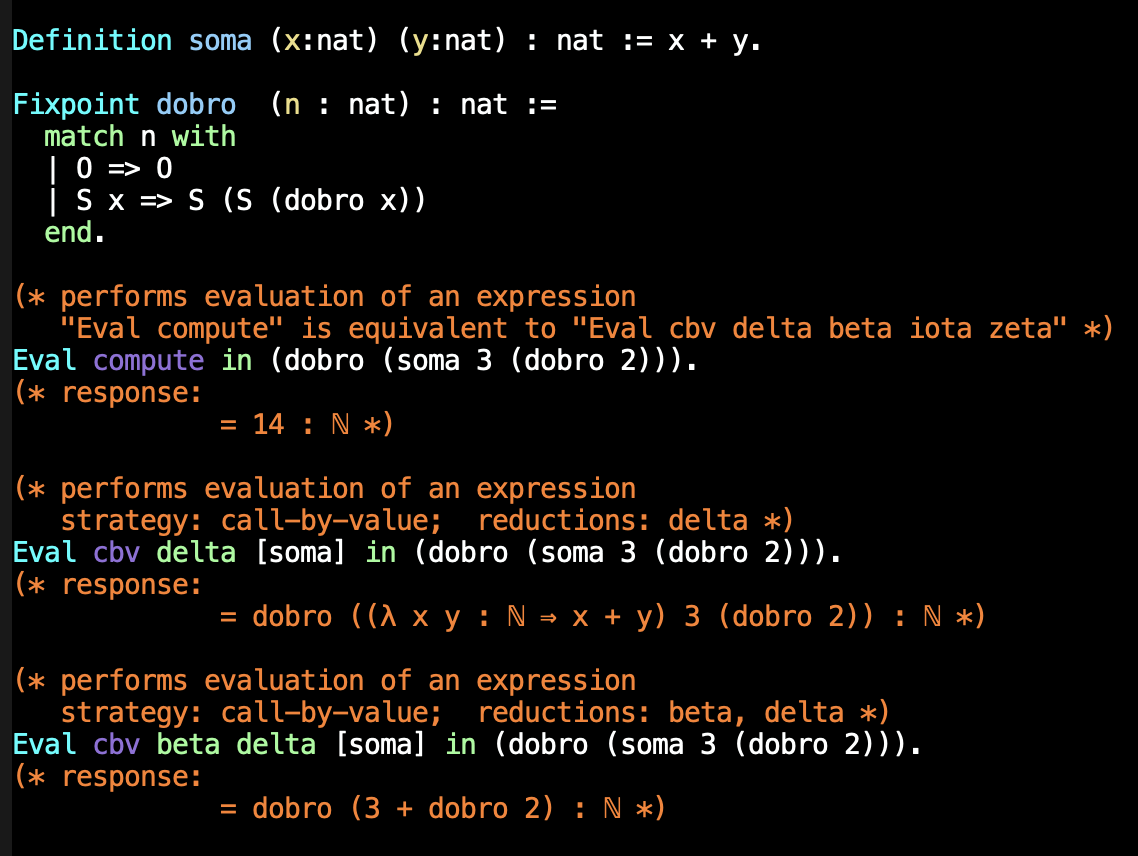
Sessão Laboratorial
É aconselhável instalar o Coq no seu computador. Sugerimos que instale o CoqIDE.
Se não tiver o Coq instalado, poderá usar o JsCoq que carrega Coq inteiramente no seu browser, sem instalar nada.
O ficheiro lesson1.v contém muitos exemplos comentados e algumas provas para completar. Carregue este ficheiro no sistema Coq, analise atentamente os exemplos e resolva os exercícios propostos.
Exercícios: Encontrará exercícios adicionais em Coq(1).pdf.