MFP

Índice
| Métodos Formais em Engenharia de Software |
|---|
| Cálculo de Sistemas de Informação |
| Programação Ciber-física |
| Verificação Formal |
| Projecto em MFP |
| Anos anteriores |
| Calendário | Sumários |
| Alumni |
Uma máquina de estados para o concept ToDo em Coq
Máquinas de estados e relações de transição podem usadas para modelar a execução de sistemas de software, com múltiplas funções que alteram o estado, e estudar as suas propriedades. Vamos recuperar o exemplo do concept ToDo, usado na aula 5 (em Why 3), para ilustrar como o implementar em Coq e provar mais propriedades sobre o sistema de transição que o modela.
Carregue o ficheiro lesson4.v no assistente de prova Coq para seguir a apresentação. Analise as respostas obtidas e resolva os exercícios propostos.
O estado e operações sobre o estado
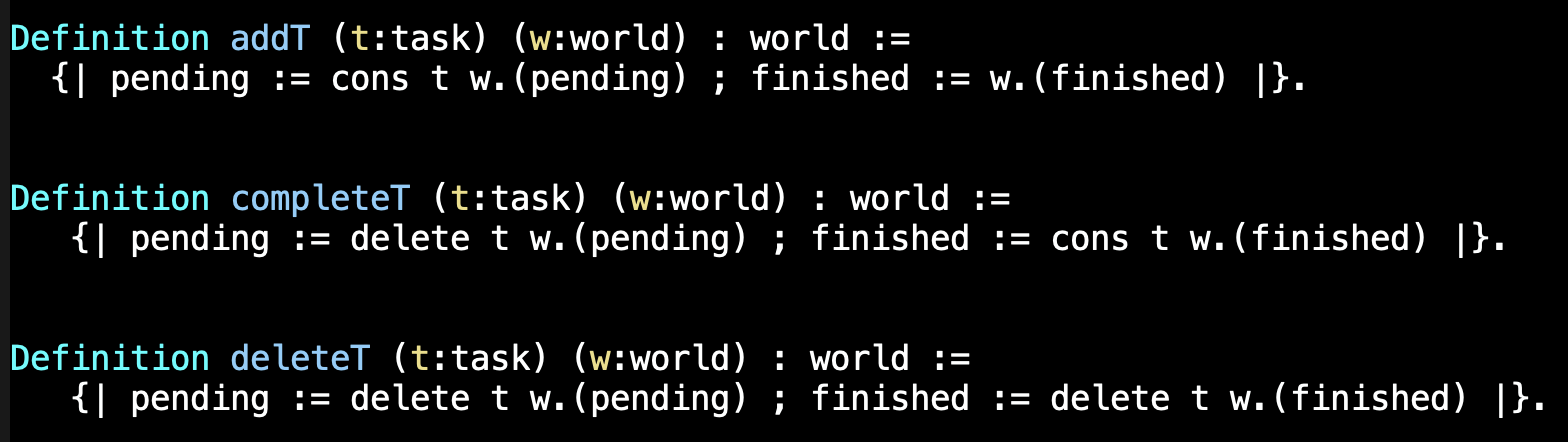
No concept ToDo o estado é um par de conjuntos de tarefas: um para as tarefas pendentes e outro para as tarefas concluídas. A API deste módulo de software consiste em três funções: addT (que adiciona uma tarefa às tarefas pendentes), completeT (que passa uma tarefa pendente para concluída) e deleteT (que excluí uma tarefa de ambas as listas). Estas funções estabelecem uma relação de transição no conjunto de estados: cada função define uma ação, realizando uma transição que leva o sistema de um estado para outro.
Vejamos como implementar o concept ToDo no sistema Coq. Vamos manter os nome usados quando este exemplo foi trabalhado em Why3 mas, para simplificar, vamos representar cada tarefa por um número natural e implementar os conjuntos em listas.
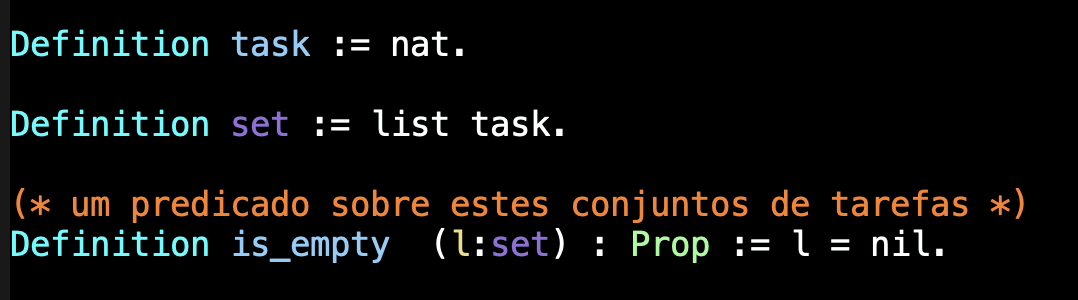
O estado é uma estrutura/record com dois conjuntos: o das tarefas pendentes e o das tarefas terminadas.

Ao definir o tipo word, as funções de seleção pending e finished ficam definidas automaticamente.
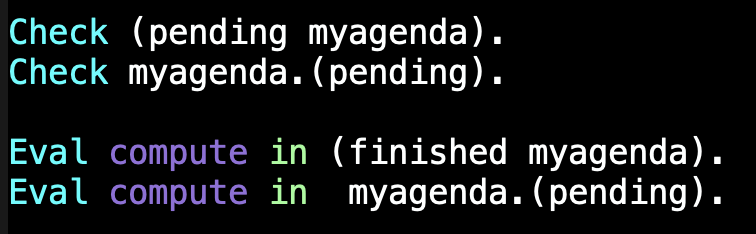
Vejamos um exemplo deste tipo, definindo a constante myagenda.

Podemos usar os seletores do record de duas formas:
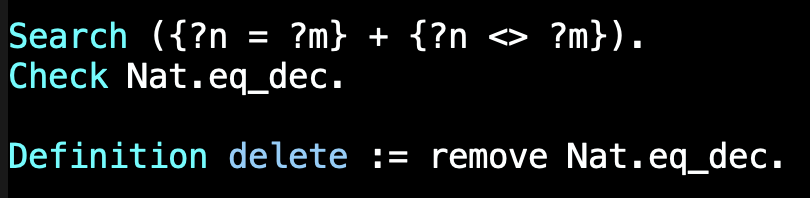
Passemos à definição das operações addT, completeT e deleteT. Para remover uma tarefa de uma lista vamos usar a função remove já definida na biblioteca List carregada,

mas esta função é genérica e recebe como argumento o predicado (decidível) usado para testar se dois elementos são iguais ou diferentes.

Podemos definir a função delete, para lista de naturais, à custa da remove, passando como argumento o teste de igualdade para os naturais.
As ações addT, completeT e deleteT podem ser definidas como funções que alteram o estado, assim:
Vamos ter um invariante sobre o estado, proibindo as tarefas de pertencer, simultaneamente, à lista de tarefas pendentes e de tarefas concluídas.

Note que In é um predicado definido na biblioteca List como uma função.


Vejamos agora como cada operação preserva o invariante e cumpre o seu contracto. Por exemplo, no caso da operação addT temos:
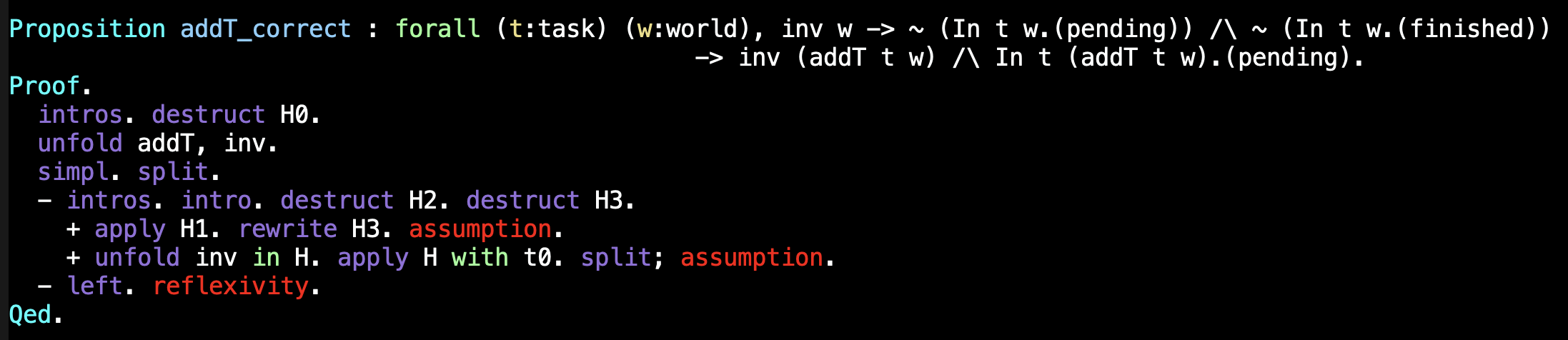
Analise no ficheiro o que fazer para provar a correção das outras duas operações e complete as provas em falta.
O sistema de transição
Vamos agora modelar o concept ToDo num sistema de transição, para depois estudar as suas propriedades.
Começamos por definir um predicado que caracteriza um estado inicial.

A relação de transição pode ser definida indutivamente pela seguinte relação.

O fecho transitivo e reflexivo da relação de transição pode ser definido pelo seguinte predicado indutivo.

Será simples provar (por indução na relação) que a relação de transição em zero ou mais passos preserva o invariante.

A noção de estado alcançável pode ser implementada pelo seguinte predicado.

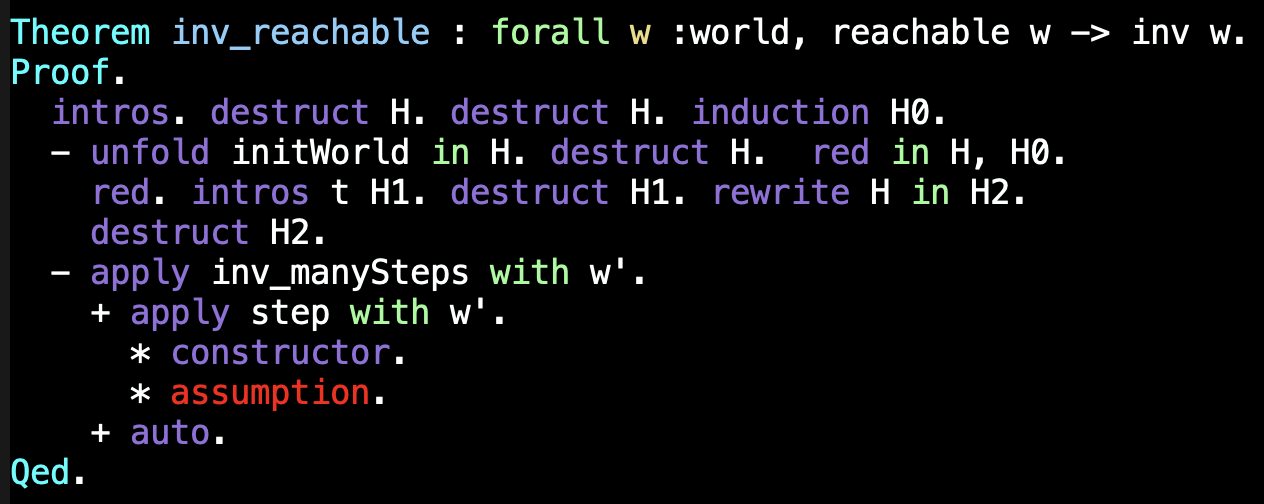
Estamos finalmente em condições de provar que todos os estados alcançáveis preservam o invariante.
Outras propriedades
As propriedades até aqui demonstradas já tinham sido provadas em Why3 de uma forma quase automática. Isso deve-se ao facto de as provas serem relativamente simples e de não termos explodado, no sistema Coq, a codificação de táticas automáticas que poderiam ajudar bastante o processo de prova. Há no entanto outro tipo de propriedades com que o Why3 teria mais dificuldade em lidar, e possivelmente não se resolveriam de forma automática.
Vejamos então outro tipo de propriedades que o sistema satisfaz. Começe por provar o seguinte lema.

Este lema vai ser útil para provar a seguinte propriedade: “Toda a tarefa que esteja no conjunto das tarefas terminadas tem que ter estado, previamente (em alguma configuração passada), no conjunto das tarefas pendentes. “

Analise a prova e resolva os dois exercícios finais propostos no ficheiro.