MFP

Índice
| Métodos Formais em Engenharia de Software |
|---|
| Cálculo de Sistemas de Informação |
| Programação Ciber-física |
| Verificação Formal |
| Projecto em MFP |
| Anos anteriores |
| Calendário | Sumários |
| Alumni |
Verificação de Algoritmos Funcionais em Coq
O sistema Coq é baseado num formalismo que é ao mesmo tempo uma lógica muito expressiva e uma linguagem de programação com um sistema de tipos muito rico. É portanto uma boa plataforma para verificação formal de algoritmos funcionais. O Coq possui mesmo um mecanismo de extração de programas, que permite extrair o programa a partir da prova da sua especificação (filtrando o conteúdo computacional dos objectos de prova).
Tipos de Dados para Programação
Vejamos alguns exemplos de tipos dados úteis para programação já definidos no sistema.

| Algumas operações sobre o tipo bool também são fornecidas: andb (com notação infixa &&), orb (com notação infixa ** | ), **xorb, implb e negb. |

A soma construtiva {A}+{B} de duas proposições A e B.

O tipo sumbool pode ser usado para definir uma construção “if-then-else”. O sistema Coq aceita a sintaxe “if test then… else …“ quando test tem do tipo bool ou {A}+{B}, com proposições A e B. O seu significado é
match test with
| left H => ...
| right H => ... end.
Podemos chamar a {P}+{~P} o tipo dos “predicados decidíveis”:

Aqui está um exemplo de uma função que verifica se um elemento está numa lista.

Tipos $\Sigma$
O sistema de tipos de Coq permite combinar um tipo e um predicado sobre esse tipo. O tipo de dados obtido representa o subconjunto do tipo cujos elementos verificam o predicado.

A convenção sintática para (sig A P) é a construção {x:A | P x}. (O predicado P é a função característica deste conjunto). Podemos construir elementos deste conjunto como (exist x p) sempre que tivermos uma testemunha x:A e a sua justificação p:(P x). Um valor do tipo {x:A | P x} deve conter um componente computacional que diz como obter um valor v e um certificado, uma prova de que v satisfaz o predicado P.
Em termos técnicos, diz-se que sig é uma “soma dependente” ou um Σ-type.
Também existe uma variante sig2 com dois predicados:
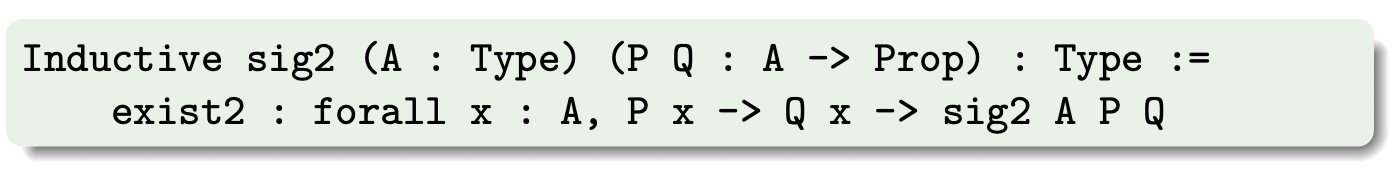
| A notação para (sig2 A P Q) é **{x:A | P x & Q x}**. |
Sessão Laboratorial
Vamo-nos agora focar na correção de programas funcionais, tendo por base alguns exemplos. Carregue o arquivo lesson3.v no assistente de prova Coq para correr os exemplos que a seguir de apresentam. Analise as respostas obtidas e resolva os exercícios propostos.
Correção de Programas Funcionais
Em Coq existem duas abordagens para definir funções e fornecer provas de que elas satisfazem uma determinada especificação:
- Definir essas funções com uma especificação fraca e depois adicionar lemas complementares que demonstram a sua correção. Por exemplo, definimos uma função f : A → B e provamos uma afirmação da forma (∀x:A, R x (fx)), onde R é uma relação que codifica o comportamento de entrada/saída pretendido da função.
-
Fornecemos uma especificação forte da função: **f : A → {v:B R x v}** . O tipo desta função afirma diretamente que a entrada é um valor x do tipo A e que a saída é a combinação de um valor v do tipo B e uma prova de que v satisfaz (R x v).
Vamos começar por ilustrar estas duas abordagens com dois exemplos muito simples: as funções head e last que dão, respectivamente, o primeiro e o últimos elemento de uma lista. Estas duas funções embora muito simples introduzem uma dificuldade adicional: são funções parciais que só se podem aplicar a listas não vazias.
Parcialidade
O sistema Coq não permite a definição de funções parciais (ou seja, funções que apresentam erros em tempo de execução para determinadas entradas). No entanto, podemos enriquecer o domínio da função com uma pré-condição que garanta que as entradas inválidas sejam excluídas.
Uma função parcial do tipo A → B pode ser descrita com um tipo da forma (∀x:A,(P x) → B), onde P é um predicado que descreve o domínio da função.
A aplicação de uma função deste tipo requer dois argumentos: um termo t do tipo A e uma prova da pré-condição (P t).
Vajamos o que acontece no caso da função head.

Para superar esta dificuldade precisamos de acrescentar a pré-condição de que a lista não é vazia.

Ao escrever este comando uma prova é lançada e temos construir um termo do tipo l<>nil -> A. Podemos continuar a fazer isso por análise de casos sobre a lista l, usando match, mas neste caso o tipo de retorno do “match” passa a ser uma função de uma prova da pré-condição para o tipo do resultado. Uma ramificação inválida do “match” leva a uma contradição lógica (viola a pré-condição).

“refine term“ é uma tática que se pode aplicar a qualquer objectivo de prova. É semelhante à tática “exact term” com uma diferença: o utilizador pode colocar buracos no termo (representados por _). Serão gerados tantos sub-objectivos de prova quantos buracos no termo.
Especificação (fraca) + Prova de Correção.
A especificação da função head pode então ser feita do seguinte modo:

A sua correção é atestada pelo seguinte lema.

Extração de Programas
O sistema de tipos do Coq (CIC) é muito mais rico do que o das linguagens de programação convencionais. As funções CIC podem conter subtermos correspondentes a provas que, em termos práticos, não têm interesse em relação ao valor final. Os cálculos feitos nas provas correspondem a verificações que devem ser feitas em tempo de compilação, enquanto o cálculo dos dados reais precisa ser feito para cada valor passado às funções em tempo de execução.
O Coq tem um mecanismo de extração que faz a filtragem do conteúdo computacional dos termos, e os converte para uma linguagem de programação alvo (Ocaml, Haskell ou Scheme). A distinção entre os sorts Prop e Set é utilizada para distinguir os aspectos lógicos (que devem ser descarregados durante a extração) dos aspectos computacionais (que devem ser mantidos).
O framework de extração deve ser carregado explicitamente.



Também é possível utilizar os tipos e construtores da linguagem de programação alvo. Por exemplo, podemos querer usar as listas nativas do Haskell em vez do Coq.

Especificação (forte) com $\Sigma$-types
Usando tipos Σ, podemos escrever restrições de especificação no tipo de uma função, restringindo o tipo do contradomínio aos valores que satisfazem a especificação.
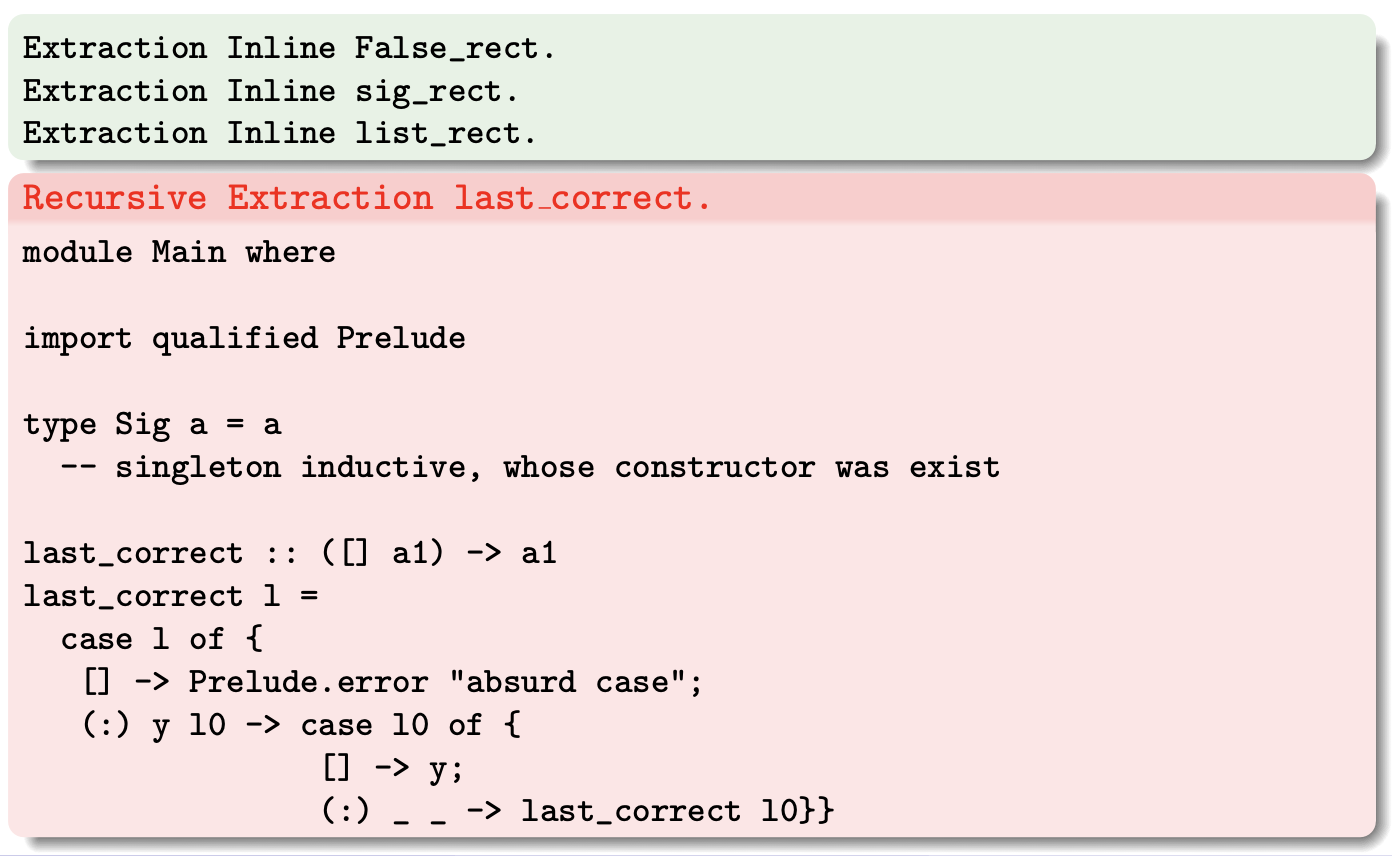
Vejamos o predicado Last definido indutivamente e o teorema que especifica a função que fornece o último elemento de uma lista.

Ao provar este teorema construímos um habitante deste tipo, e então podemos extrair o conteúdo computacional desta prova, e obter uma função que satisfaz a especificação.

Caso de Estudo: o Algoritmo Insertion Sort
Vamos agora ver o exemplo do algoritmo de ordenação insertion sort para uma lista de inteiros.
Numa lista ordenada cada dois elementos consecutivos são compatíveis com a relação ≤. Podemos codificar isso definindo indutivamente o predicado Sorted.

Como sabemos, a lista produzida por um algoritmo de ordenação deve ser uma permutação da lista original. Para codificar a relação de permutação, em vez de uma definição indutiva, definiremos a relação utilizando uma função auxiliar que conta o número de ocorrências dos elementos.

Uma lista é uma permutação de outra quando contém exatamente o mesmo número de ocorrências de para cada elemento.

A relação de permutação é uma relação de equivalência.

Analise as provas e prove as seguintes propriedades.

O algoritmo insertion sort ordena uma lista iterando uma função insert que insere um elemento numa lista ordenada.

A correção deste algoritmo ficará demonstrada pela prova do seguinte teorema:

Para realizar esta prova vamos certamente precisar de lemas auxiliares… Façamos uma tentativa de demonstração prospectiva:

Parece claro que serão úteis os seguintes lemas:

Para prová-los, os seguintes lemas sobre a função count podem também ser úteis.

Podemos agora terminar a prova de correção do insertion sort

Uma outra abordagem ao problema de ordenação seria dar uma especificação forte (usando tipos $\Sigma$) para a função de ordenação. Tirando proveito do que já foi feito podemos completar esta prova e extrair o programa.

Exercícios: Encontrará exercícios adicionais em Coq(3).pdf.