MFP

Índice
| Métodos Formais em Engenharia de Software |
|---|
| Cálculo de Sistemas de Informação |
| Programação Ciber-física |
| Verificação Formal |
| Projecto em MFP |
| Anos anteriores |
| Calendário | Sumários |
| Alumni |
Raciocínio Indutivo no Sistema Coq
A indução é uma técnica que nos permite definir e raciocinar com objectos que são estruturados (de uma forma bem fundada) e finitos (embora arbitrariamente grandes). A indução explora a natureza finita e estruturada desses objectos para superar a sua complexidade arbitrária.
Quando um conjunto é definido indutivamente, entendemos que ele é “construído de baixo para cima” por um conjunto de construtores básicos. Os elementos de tal conjunto podem ser decompostos de forma única em “elementos menores” de maneira bem fundada. Isto dá-nos princípios de prova por indução e definição de funções com recursores.
Tipos Indutivos em Coq
Podemos definir um novo tipo $T$ indutivamente, declarando os seus construtores com os respectivos tipos, que devem ter a forma: $\tau_{1} \to \ldots \to \tau_{n} \to T$ , com $n\geq 0$, onde $T$ pode apenas ocorrer em posições positivas de $\tau_i$.
Os construtores (que são as regras de introdução do tipo $T$) são formas canónicas de construir um elemento do tipo $T$. O tipo $T$ definido é o menor conjunto fechado para as suas regras de introdução. Portanto, os seus habitantes são os objetos que podem ser obtidos por um número finito de aplicações dos construtores do tipo.
Vamos focar-nos no exemplo dos número naturais, nat, com dois construtores: o zero, O, e o sucessor, S.

Para programar e raciocinar sobre um tipo indutivo precisamos de meios para analisar os seus habitantes. As regras de eliminação para os tipos indutivos fornecem formas de utilizar os objetos do tipo indutivo para definir objetos de outros tipos, e estão associadas a novas regras computacionais.
Um tipo indutivo, para além dos seus construtores, vem também equipado com um recursor que pode ser usado para definir funções e provar propriedades sobre o tipo. Quando um tipo indutivo é definido, automaticamente é gerado um esquema para prova por indução e um esquema para recursão primitiva (materializado por constantes que são acrescentadas ao ambiente global do sistema).
O recursor é uma constante $\mathbf{R}T$ que representa o _princípio de indução estrutural para os elementos do tipo indutivo $T$, e a regra de cálculo associada a ele define um esquema recursivo seguro (que não introduz não terminação) para programação.
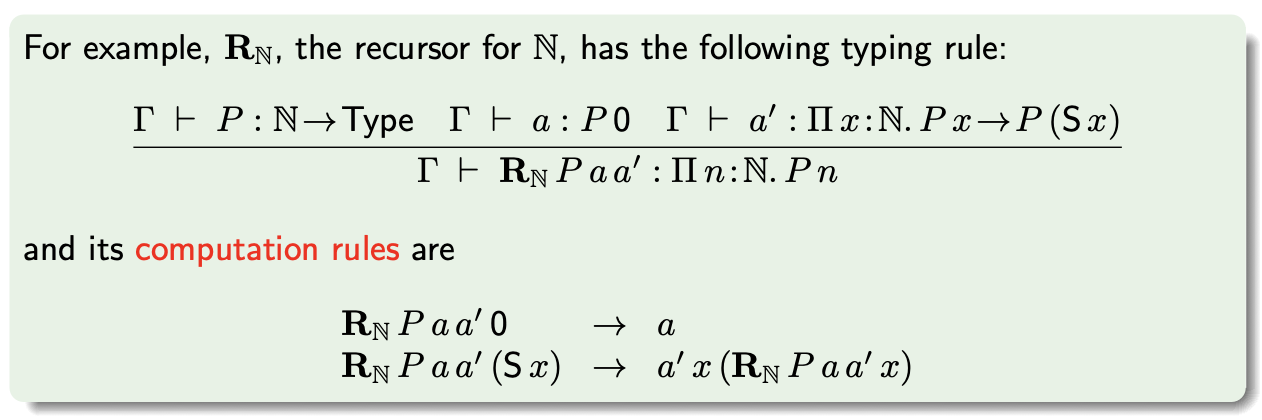
Com este recursor é possível definir um princípio de prova por indução e um princípio de recursão primitiva.
O esquema de prova por indução pode ser obtido do recursor definindo $P$ como sendo do tipo $\mathbb{N}\to \mathsf{Prop}$.

Este é o conhecido princípio de indução sobre números naturais, que permite provar propriedades da forma $\forall n: \mathbb{N}. (P n)$, por indução em $n$.
O esquema de recursão primitivo pode ser obtido configurando $P : \mathbb{N} \to \mathsf{Set}$.
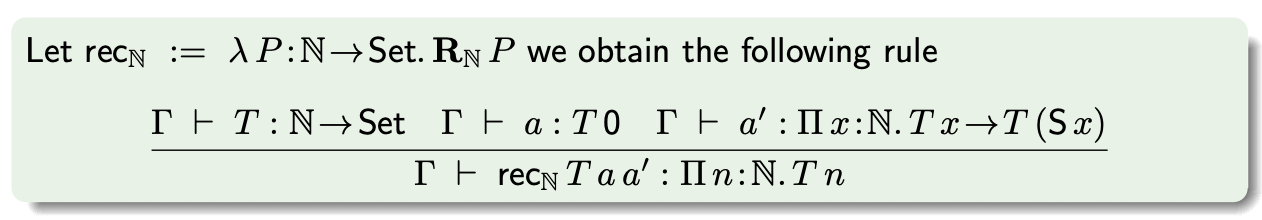
Podemos definir funções usando a recursão primitiva

Esta abordagem oferece uma maneira segura de expressar recursão sem introduzir termos que não terminam.
Vejamos como a declaração do tipo indutivo nat introduz no ambiente do sistema Coq, não apenas os construtores O e S, mas também os eliminadores (nat_rect, nat_ind e nat_rec) apresentados acima.

Análise de Casos e Recursão Geral
Codificar funções recursivas em termos de constantes de eliminação é uma maneira segura de expressar recursão (i.e., sem introduzir objetos não normalizáveis), mas está muito longe da forma como costumamos programar. Em vez disso, geralmente usamos recursão geral e análise de casos.
A análise de casos fornece uma regra de eliminação para tipos indutivos. Por exemplo, sendo $n: \mathbb{N}$, podemos definir um objecto $(\mathsf{match \ } n \mathsf{\ with \ } { 0 \Rightarrow b1 | (S x) \Rightarrow b2})$ dum outro tipo σ dependendo do construtor que for usado para introduzir $n$.

As linguagens de programação funcional admitem recursão geral, permitindo que funções recursivas sejam definidas por meio de concordância de padrões e um operador de ponto fixo geral para codificar chamadas recursivas.

Por exemplo, a função double pode também ser definida assim.

É claro que esta abordagem abre as portas para a introdução de objectos não normalizáveis.
A não terminação do processo de computação num sistema com tipos dependentes (de termos) tem impacto na decidibilidade do algoritmo type-checking (que é o núcleo sistema Coq), devido à verificação da conversibilidade entre tipos que pode exigir computação com funções recursivas.

|
Em Coq não é permitido definir funções que não terminam. Uma maneira usual de garantir a terminação de expressões de ponto fixo é impor restrições sintáticas, restringindo todas as chamadas recursivas a serem aplicadas a termos estruturalmente menores que o argumento formal da função. Outra forma de garantir terminação é aceitar uma função de medida (de indução) que especifique como o argumento “diminui” entre chamadas recursivas.
Definições Indutivas
No sistema Coq as definições indutivas estão por todo o lado. Por exemplo, as operadores relacionais e as próprias conectivas lógicas estão definidas como tipos indutivos.
Relações
Em Coq, a igualdade entre dois habitantes x e y do mesmo tipo A, denotada x = y, é definida como uma família de predicados recursivos “ser igual a x”, parametrizados tanto por x quanto por seu tipo A. Esta família de tipos possui apenas uma regra de introdução, que corresponde à reflexividade.

O princípio de indução gerado é o seguinte:
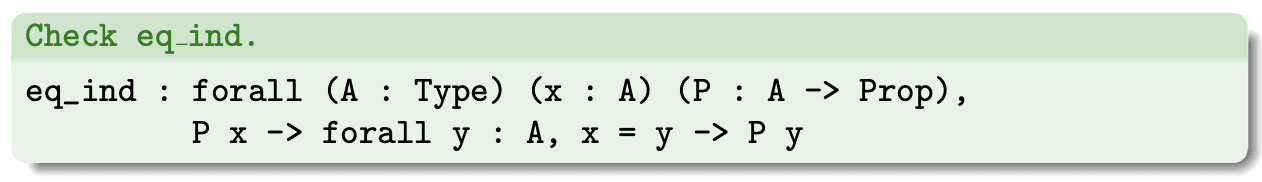
Note que a sintaxe “x = y” é uma notação alternativa de “eq x y”, e que o parâmetro A está implícito, pois pode ser inferido de x.

Outras relações também são introduzidas como uma família indutiva de proposições. Por exemplo, a relação de ordem n ≤ m nos números naturais é definida da seguinte forma:

Esta definição introduz a relação binária n ≤ m como a família de predicados unários “ser maior ou igual a um dado n”, parametrizado por n. Note como n é um parâmetro geral, enquanto o segundo argumento de le é um índice. Uma notação alternativa para “le x y” é “x <= y”.
Repare como os constructores deste tipo indutivo podem ser vistos como as regras de introdução para a relação “<=” no sistema de prova. Na verdade, um objeto do tipo n ≤ m nada mais é do que uma prova construída usando os construtores le_n e le_S.
Conectivas Lógicas
No sistema Coq, a maioria das conectivos lógicas são definidas como tipos indutivos. As excepções são: as conectivas ⇒ e ∀ que são diretamente representados pelos tipos → e Π; a negação que é definida como a implicação do absurdo; e a equivalência que é definida como a conjunção de duas implicações.


Os construtores são as regras de introdução. O princípio da indução fornece as regras de eliminação. Todas as regras da lógica intuicionista (que vimos na aula passada) são deriváveis.
Sessão Laboratorial
Vamos começar por realçar alguns aspectos práticos do sistema Coq que nos parecem relevantes para a sua utilização.
Poderá experimentar o que a seguir se explica, correndo no Coq o ficheiro lesson2a.v e analisando as respostas obtidas.
Notation, Overloading and Interpretation scopes
Para simplificar a escrita de expressões, o Coq permite introduzir notações alternativas através do comando Notation. Algumas notações podem ser sobrecarregadas. O comando Locate permite encontrar a função escondida atrás de uma notação.

Para lidar com a sobrecarga, o sistema Coq fornece uma noção de interpretation scopes, que definem como as notações são interpretadas.
Os scopes podem ser abertos e vários scopes podem estar abertos ao mesmo tempo. Quando uma determinada notação tem diversas interpretações, o scope aberto mais recentemente tem precedência.
Pode-se usar a sintaxe (term)%key para vincular a interpretação do term ao scope key.
Arguments Implícitos
Em muitos termos algumas informações de tipo são redundantes, pois podem ser inferidas do restante termo. Um subtermo pode ser substituído pelo símbolo _ se puder ser inferido de outras partes do termo.

O mecanismo de argumentos implícitos permite evitar usar _ nas expressões Coq. Podemos activar este mecanismo correndo o comando Set Implicit Arguments.

Como pode constatar ao correr estas definições, os argumentos que podem ser inferidos são automaticamente determinados e declarados como argumentos implícitos quando uma função é definida.
Além disso,

|
Irrelevância da Prova
No processo de desenvolvimento de uma prova, um termo (de prova) vai sendo construído e quanto a prova termina, e é guardada, é feito o seu type-checking e o identificador correspondente ao nome da prova fica definido com termo da prova. No entanto, esta definição é opaca, i.e., não pode ser “aberta” (ou seja, usada na redução $\delta$).
Seja $P$ uma proposição e $t$ um termo de tipo $P$.

-
Uma definição feita com Definition ou Let é transparente: seu valor t e tipo P são visíveis para uso posterior.
-
Uma definição feita com Teorema, Lema, etc., é opaca: apenas o tipo P e a existência do valor t ficam visíveis para uso posterior.
Bibliotecas do Coq
No desenvolvimento de provas pode-se tirar proveito das bibliotecas disponibilizadas pelo sistema Coq.
- A biblioteca inicial: contém noções lógicas elementares e tipos de dados. Constitui o estado básico do sistema diretamente disponível na execução do Coq.
- As bibliotecas standard, de uso geral, contendo vários desenvolvimentos sobre conjuntos, listas, aritmética, etc. Estas bibliotecas vêm com o sistema e seus módulos são acessíveis diretamente através do comando Require Import.
- As bibliotecas disponibilizadas pela comunidade de utilizadores do sistema Coq, que estão disponíveis para download.
Nas bibliotecas standard os tipos de dados mais comuns são representados como tipos indutivos e os packges fornecem uma variedade de propriedades, funções e teoremas em torno desses tipos de dados.

Pesquisa de Propriedades
No desenvolvimento de provas podemos usar propriedades que estão disponíveis no ambiente de prova. Os comandos que nos permitem fazer pesquinas dessas propriedades são naturalmente úteis.
- Search ident - exibe o nome e o tipo de todos os teoremas cuja conclusão tem a forma (ident t1 .. tn) ou que têm ident no nome.
- SearchPattern pattern - exibe o nome e o tipo de todos os teoremas que concordam com o padrão indicado.
- SearchRewrite pattern - exibe o nome e o tipo de todos os teoremas cuja conclusão é uma igualdade em que um dos lados corresponde ao padrão.

Desenvolvimento de Provas
O sistema Coq fornece um enorme conjunto de táticas de prova, combinadores de táticas e comandos, que poderão ser consultados (em todos os seus detalhes e variantes) no referencie manual. Destacamos abaixo algumas das mais relevantes.
No ficheiro lesson2b.v vai encontrar muitos exemplos comentados e algumas provas para completar. Carregue este ficheiro no sistema Coq, analise atentamente os exemplos e resolva os exercícios propostos.
Táticas básicas

|
Táticas para lidar com as conectivas lógicas
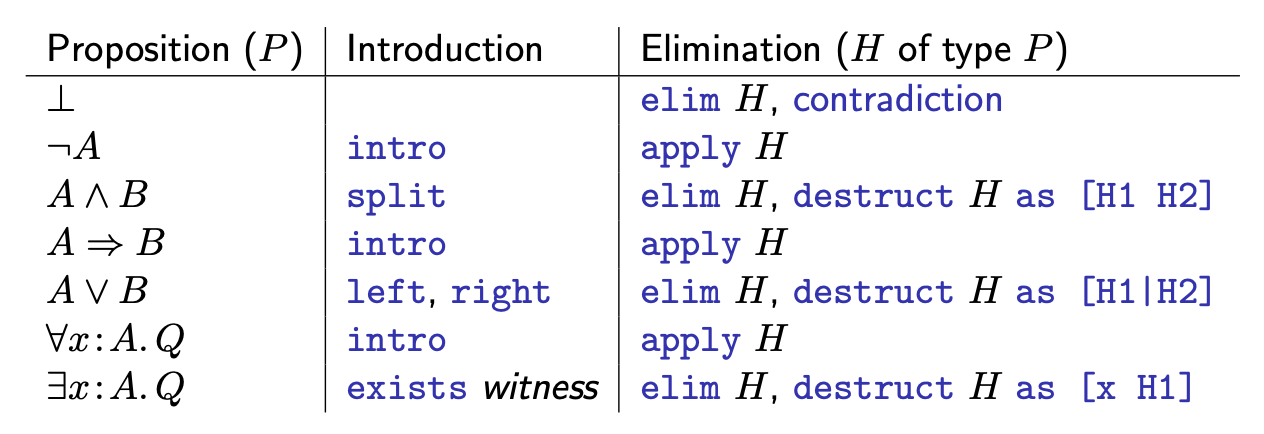
|
Táticas para lidar com igualdade

|
Táticas para lidar com a conversão de termos

|
Táticas para raciocínio indutivo

|
Mais algumas táticas e comandos úteis

|
Combinadores de táticas
As táticas podem ser combinadas em táticas mais poderosas usando combinadores de táticas (tacticals)

|
Táticas automáticas

|
As táticas automáticas utilizam repositórios de teoremas, e é possível gerir estes repositórios para controlar automação das táticas.
Exercícios: Encontrará exercícios adicionais em Coq(2).pdf.