MFP

Índice
| Métodos Formais em Engenharia de Software |
|---|
| Cálculo de Sistemas de Informação |
| Programação Ciber-física |
| Verificação Formal |
| Projecto em MFP |
| Anos anteriores |
| Calendário | Sumários |
| Alumni |
Verificação Formal: Aula 3
Temporal Logic of Actions
O problema com a lógica temporal linear apresentada anteriormente é que apenas pode ser usada para especificar as propriedades desejadas para o algoritmo. O algoritmo em si tem que ser especificado com um sistema de transição, que na maioria dos model checkers é descrito recorrendo a uma linguagem específica. Leslie Lamport, que também recebeu um prémio Turing em 2013, propôs uma variante da lógica temporal linear, designada Temporal Logic of Actions (TLA), que permite especificar não só as propriedades desejadas para um algoritmo, mas também o sistema de transição que modela o algoritmo. A grande novidade é a possibilidade de especificar predicados de transição (designados actions) que referem não só as variáveis do algoritmo, mas também o valor destas variáveis no estado seguinte (usando o nome da variável com uma plica). Combinando actions com o operador $\square$ conseguimos especificar quais os comportamentos válidos de um sistema de transição. A especificação de uma action tem tipicamente fórmulas de três naturezas distintas: guardas, que especificam quando é que pode ocorrer; efeitos, que especificam como se alteram certas variáveis quando ocorre; e frame conditions, que especificam quais as variáveis que não se alteram.
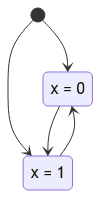
Considere por exemplo o seguinte sistema de transição.
Este sistema tem apenas dois comportamentos possíveis, que são precisamente os únicos comportamentos que satisfazem a seguinte fórmula.
\[(x = 0 \vee x = 1) \wedge \square ((x = 0 \wedge x' = 1) \vee (x = 1 \wedge x' = 0))\]Para verificar se um algoritmo satisfaz uma determinada propriedade bastará então verificar se a mesma é implicada por esta fórmula que descreve o seu comportamento. Por exemplo, para verificar que neste sistema de transição $x$ tem recorrentemente o valor 0 basta verificar a validade da seguinte fórmula.
\[(x = 0 \vee x = 1) \wedge \square ((x = 0 \wedge x' = 1) \vee (x = 1 \wedge x' = 0)) \Rightarrow \square \lozenge (x = 0)\]O TLA também permite verificar se um algoritmo refinamento é um refinamento de outro, isto é, se um algoritmo é uma implementação de outro algoritmo mais abstrato. O refinamento mais típico consiste em acrescentar mais variáveis e transições que afetem apenas essas novas variáveis. Por exemplo, um relógio com ponteiros de horas, minutos e segundos, é um refinamento de um relógio com apenas ponteiros de horas e minutos. Algumas das transições que irão existir no algoritmo mais refinado não são visíveis no algoritmo mais abstrato. No exemplo do relógio esse é o caso dos movimentos do ponteiro dos segundos. Sendo assim, qualquer especificação de um algoritmo deve permitir que existam sempre passos de stuttering, onde nenhuma variável muda de valor, passos esses que irão corresponder às transições que afetam apenas as novas variáveis introduzidas no refinamento.
Para obrigar que existam sempre passos de stuttering o TLA não deixa usar as actions de qualquer forma. Em particular quando uma action é usada dentro do operador $\square$ irá sempre ser enquadrada numa disjunção que também admite um passo de stuttering. Dada uma action $A$, a action $[A]_t \doteq A \vee t’ = t$ significa que ou $A$ ocorreu ou a expressão $t$ manteve o seu valor ($t’$ é a expressão que resulta de acrescentar uma plica a todas as variáveis em $t$). Em particular se usarmos como expressão um tuplo com todas as variáveis de estado, então $[A]_t$ será válida sse $A$ for válida ou ocorreu um passo de stuttering.
Pela mesma razão o TLA também não suporta o operador $\bigcirc$, pois com esse operador seria possível escrever fórmulas que impediriam o stuttering nalgumas situações.
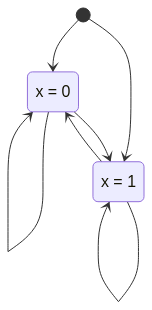
No caso do exemplo anterior, a especificação do comportamento em TLA seria então
\[\begin{array}{c} (x = 0 \vee x = 1) \wedge \square [(x = 0 \wedge x' = 1) \vee (x = 1 \wedge x' = 0)]_{\langle x,y \rangle}\\ \equiv\\ (x = 0 \vee x = 1) \wedge \square ((x = 0 \wedge x' = 1) \vee (x = 1 \wedge x' = 0) \vee \langle x',y' \rangle = \langle x,y \rangle)\\ \equiv\\ (x = 0 \vee x = 1) \wedge \square ((x = 0 \wedge x' = 1) \vee (x = 1 \wedge x' = 0) \vee (x' = x \wedge y' = y)) \end{array}\]o que corresponderia ao seguinte sistema de transição.
A outra possibilidade de utilizar actions é dentro do operador $\mathsf{ENABLED}$: dada uma action $A$ este operador transforma-a num predicado normal que determina se $A$ pode ocorrer. Por exemplo $\mathsf{ENABLED}\ (x = 0 \wedge x’ = 1) \equiv x = 0$.
Outra diferença do TLA em relação à lógica temporal linear apresentada anteriormente é que o TLA é uma lógica de primeira ordem, ou seja permite a utilização de quantificadores. A gramática da lógica TLA é então definida da seguinte forma.
\[\begin{array}{lcl} \mathit{formula} & \doteq & \mathit{predicate}\\ & \mid & \mathsf{ENABLED}\ \mathit{action}\\ & \mid & \neg \mathit{formula}\\ & \mid & \mathit{formula} \wedge \mathit{formula}\\ & \mid & \exists \mathit{variable} \cdot \mathit{formula}\\ & \mid & \square\ \mathit{formula}\\ & \mid & \square [\mathit{action}]_\mathit{function} \end{array}\]Nesta definição, $\mathit{predicate}$ representa um predicado arbitrário envolvendo variáveis de estado (variáveis flexíveis) ou variáveis quantificadas (variáveis rígidas), $\mathit{action}$ é um predicado de transição arbitrário envolvendo variáveis de estado (com ou sem plica) ou variáveis quantificadas, e $\mathit{function}$ é uma função (expressão) arbitrária envolvendo variáveis de estado.
A semântica do TLA pode ser definida da seguinte forma (onde $F$ e $G$ representam fórmulas arbitrárias, $P$ um predicado arbitrário, e $A$ uma action arbitrária). Note que, ao contrário dos predicados normais, a validade das actions tem que ser determinada em pares de estados consecutivos.
\[\begin{array}{lcl} s_0,s_1,\ldots \models P & \equiv & s_0 \models P\\ s_0,s_1,\ldots \models A & \equiv & s_0,s_1 \models A\\ s_0,s_1,\ldots \models \mathsf{ENABLED}\ A & \equiv & \exists s_1 \cdot s_0,s_1 \models A\\ s_0,s_1,\ldots \models \neg F & \equiv & s_0,s_1,\ldots \not\models F \\ s_0,s_1,\ldots \models \exists x \cdot F & \equiv & \exists x \cdot s_0,s_1,\ldots \models F \\ s_0,s_1,\ldots \models F \wedge G & \equiv & s_0,s_1,\ldots \models F \wedge s_0,s_1,\ldots \models G\\ s_0,s_1,\ldots \models \square F & \equiv & \forall i \ge 0 : s_i,s_{i+1},\ldots \models F \\ s_0,s_1,\ldots \models \square [A]_t & \equiv & \forall i \ge 0 : s_i,s_{i+1},\ldots \models A \vee t' = t \end{array}\]Exercício: especifique o seguinte algoritmo usando TLA.
var r : integer = n;
0: if r < 0 then 1: r := -r
2:
Exercício: especifique o seguinte algoritmo usando TLA.
var x : integer = 0
procedure increment;
begin
0: x := x + 1
1: end;
increment || increment
Exercício: especifique o seguinte algoritmo usando TLA.
var
sem : boolean = true;
procedure process;
begin
0: while true do
begin
(* idle *)
1: repeat until sem;
sem := false;
(* critical *)
2: sem := true;
end
end;
process || process
A linguagem TLA+
A lógica TLA está na base da linguagem de especificação TLA+, que enriquece a lógica base com primitivas para estruturação de especificações de grande dimensão. Por exemplo, permite introduzir definições auxiliares e tem um sistema de módulos. É uma linguagem não tipada, podendo as variáveis tomar valores tais como inteiros, conjuntos, funções, tuplos ou records. A maioria dos operadores tem uma sintaxe ASCII relativamente standard, sendo que para alguns é usada a sintaxe do LaTeX (também criado por Leslie Lamport). Para usar algumas operações pode ser necessário importar um dos módulos pré-definidos. Um sumário da sintaxe do TLA+ pode ser encontrado aqui.
Uma especificação em TLA+ tem que ser escrita entre os delimitadores ---- MODULE name ---- e ==== (podem ser usados mais - e =). Para introduzir uma definição usa-se o ==. A sintaxe dos vários operadores usados nas definições pode ser consultada no documento referido acima. Para além de permitir introduzir definições, o TLA+ tem as seguintes palavras reservadas:
EXTENDS, que serve para importar módulos.CONSTANTS, que serve para declarar quais os nomes dos parâmetros constantes do algoritmo.ASSUME, que serve para especificar assunções sobre os referidos parâmetros.VARIABLES, que serve para declarar quais as variáveis flexíveis que definem o estado do algoritmo.
Como a linguagem é não-tipada, tuplos e sequências são equivalentes e escrevem-se entre os delimitadores << e >>. Dentro de uma action se quisermos especificar que uma expressão mantém o seu valor entre o pré- e o pós-estado podemos usar a palavra reservada UNCHANGED. Quando usada com um tuplo de variáveis permite facilmente especificar frame conditions.
Relembre o seguinte algoritmo de multiplicação de um inteiro não negativo a com um inteiro b, onde agora se assume que o corpo do ciclo executa de forma atómica.
var
r : integer = 0;
n : integer = 0;
0: while n < a do
begin
n := n + 1;
r := r + b
end
1:
Este algoritmo pode ser especificado em TLA+ da seguinte forma.
--------------------------- MODULE Multiplication ---------------------------
EXTENDS Integers
CONSTANTS a,b
ASSUME a >= 0
VARIABLES r,n,pc
TypeOK == [] (r \in Int /\ n \in Int /\ pc \in 0..1)
Init == r = 0 /\ n = 0 /\ pc = 0
WhileT ==
/\ pc = 0 /\ n < a
/\ n' = n + 1
/\ r' = r + b
/\ pc' = 0
WhileF ==
/\ pc = 0 /\ n >= a
/\ pc' = 1
/\ UNCHANGED <<r,n>>
Next == WhileT \/ WhileF
vars == <<r,n,pc>>
Algorithm == Init /\ [][Next]_vars
PartialCorrectness == [] (pc = 1 => r = a * b)
Termination == <> (pc = 1)
=============================================================================
Os parâmetros a e b deste algoritmo são declarados com a palavra reservada CONSTANTS, sendo a assunção de que a é não negativo especificada com a palavra reservada ASSUME. As variáveis do algoritmo e o respetivo program counter são declarados com a palavra reservada reservada VARIABLES. Nesta especificação importamos o módulo Integers pois é neste módulo que estão definidas as operações aritméticas sobre inteiros. A definição Algorithm contém a especificação do comportamento deste algoritmo, especificação esta que em TLA+ segue quase sempre o padrão Init /\ [][Next]_vars, onde Init é um predicado que especifica quais os valores iniciais das variáveis, Next a action que especifica a relação de transição do algoritmo, e vars um tuplo com todas as variáveis que devem permanecer inalteradas nos passos de stuttering obrigatórios. Os nomes destas definições auxiliares podem obviamente ser outros. A relação de transição Next é tipicamente uma disjunção de actions mais específicas. Neste caso temos duas actions, uma por cada transição possível entre os dois valores do program counter. Temos também três definições com propriedades para verificar sobre este algoritmo. A definição PartialCorrectness especifica a correção parcial deste algoritmo, nomeadamente que quando termina r contém o produto de a com b. A definição Termination especifica a propriedade de liveness que garante que o algoritmo termina. Como o TLA+ é uma linguagem não tipada, é frequente incluir um invariante na especificação, tipicamente chamado TypeOK, que verifica se as variáveis têm sempre o tipo esperado. Na ausência de um sistema de tipos, este invariante é muito útil para detetar erros na especificação. Note que a expressão n..m denota o conjunto com todos os inteiros entre n e m.
A ferramenta TLA+ Toolbox permite, entre outras funcionalidades, validar a correção sintática de especificações em TLA+.
Exercício: descarregue e instale a ferramenta TLA+ Toolbox e valide a sintaxe da especificação anterior.
Considere agora o seguinte algoritmo concorrente onde N processos incrementam uma variável partilhada.
var x : integer = 0
procedure increment(i : integer);
begin
0: x := x + 1
1: end;
increment(1) || ... || increment(N)
Este algoritmo pode ser especificado em TLA+ da seguinte forma.
----------------------------- MODULE Increment -----------------------------
EXTENDS Integers
CONSTANT N
ASSUME N > 0
VARIABLES x,pc
TypeOK == [] (x \in Int /\ pc \in [1..N -> 0..1])
Init == x = 0 /\ pc = [i \in 1..N |-> 0]
Increment(i) ==
/\ pc[i] = 0
/\ x' = x + 1
/\ pc' = [pc EXCEPT ![i] = 1]
Next == \E i \in 1..N : Increment(i)
vars == <<x,pc>>
Algorithm == Init /\ [][Next]_vars
Finish == \A i \in 1..N : pc[i] = 1
PartialCorrectness == [] (Finish => x = N)
Termination == <> Finish
=============================================================================
Como temos um número N arbitrário de processos vamos usar uma função para representar o estado dos respetivos program counters. O domínio desta função será o conjunto 1..N e o contra-domínio o conjunto 0..1, os dois possíveis valores para o program-counter de cada processo. Em TLA+ podemos definir uma função por compreensão com a sintaxe [x \in A |-> E] onde A é o domínio e E uma expressão envolvendo a variável x. No caso da especificação acima, esta sintaxe é usada na definição Init para definir o valor inicial da variável pc como sendo uma função que, para cada possível processo, retorna sempre o valor 0. Em TLA+ as definições auxiliares podem ser parametrizadas, como é o caso com a definição Increment(i) que define a action que especifica o comportamento do processo i. A relação de transição do algoritmo na definição Next especifica que, em cada momento, esta action tem que ser verdadeira para pelo menos um dos processos (para além de ser possível ocorrer um passo de stuttering). Na definição Increment(i) atente à expressão [pc EXCEPT ![i] = 1] que é uma forma abreviada de especificar uma função que é idêntica à função pc, excetuando para o valor i para o qual a função passa a devolver 1. Esta expressão podia também ser definida por compreensão como [x \in 1..N |-> IF x = i THEN 1 ELSE pc[x]]. Note que o condicional usado nesta expressão não é um comando de uma linguagem de programação imperativa, mas simplesmente uma sintaxe alternativa para a fórmula equivalente que poderia ser definida com as conectivas lógicas.
Exercício: especifique em TLA+ a seguinte variante do algoritmo acima, onde um dos N processos começa por fazer uma cópia local da variável partilhada antes de a incrementar, incluindo definições para o respetivo invariante de tipo.
var x : integer = 0;
procedure increment(i : integer);
var y : integer = 0;
begin
0: y := x;
1: x := y + 1
2: end;
increment(1) || ... || increment(N)
Exercício: especifique em TLA+ a seguinte variante do algoritmo de exclusão mútua com um semáforo para N > 1 processos, incluindo especificações para o respetivo invariante de tipo e para as propriedades de mutual exclusion e no starvation.
var
sem : boolean = true;
procedure process(i : integer);
begin
0: while true do
begin
(* idle *)
1: repeat until sem;
sem := false;
(* critical *)
2: sem := true
end
end;
process(0) || ... || process(N-1)
Exercício: especifique em TLA+ a seguinte variante do algoritmo de exclusão mútua de Peterson para N > 1 processos, incluindo especificações para o respetivo invariante de tipo e para as propriedades de mutual exclusion e no starvation.
var
level : array [0..N-1] of -1..N-2 = [N of -1];
last : array [0..N-2] of 0..N-1;
procedure process(i : integer);
var l : integer = 0;
begin
while true do
begin
(* idle *)
0: while l < N-1 do
begin
level[i] := l;
last[l] := i;
1: repeat until (last[l] != i or ∀ k != i . level[k] < l));
l := l+1
end
(* critical *)
2: level[i] := -1;
l := 0
end
end;
process(0) || ... || process(N-1)
O model checker TLC
A ferramenta TLA+ Toolbox inclui o model checker TLC que pode ser usado para verificar propriedades temporais de numa especificação TLA+. Este model checker utiliza uma técnica explícita semelhante à que foi descrita na aula anterior, implementada de uma forma extremamente eficiente, tirando partido do paralelismo permitido pela maioria dos processadores atuais.
O TLC não consegue verificar qualquer propriedade especificada em TLA. Quer a especificação do algoritmo quer a especificação da propriedade tem que seguir um certo padrão, que iremos descrever brevemente a seguir (mais detalhes podem ser encontrados no capítulo 14 do livro Specifying Systems). No entanto, este padrão é bastante permissivo e incluí todas as propriedades nas especificações TLA+ apresentadas anteriormente.
No caso da especificação do algoritmo assume-se que mesma segue o padrão Init /\ [][Next]_vars, onde Next é uma disjunção de actions (possivelmente no contexto de um quantificador existencial). A restrição mais importante é que quer no predicado Init, quer nas nas várias actions tem que ser definido o valor de todas as variáveis usando uma atribuição ou uma escolha não determinística da forma x \in A (no predicado Init) ou x' \in A (nas actions), sendo que A é um conjunto finito de valores. Por exemplo, na especificação do algoritmo de incremento não poderíamos ter definido o valor inicial da variável pc usando a quantificação \A i \in 1..N : pc[i] = 0. Numa action, a expressão no lado direito de uma atribuição ou escolha não determinística podem fazer referência ao novo valor de outra variável, desde que este tenha sido definido anteriormente. Este “anteriormente” significa que o TLC interpreta as conectivas lógicas numa action de forma sequencial. Todos os quantificadores usados têm também que ser bounded, ou seja a variável quantificada tem que iterar sobre um conjunto finito.
Quanto às propriedades a verificar, as mesmas tem que ser a conjunção de fórmulas TLA que pertencem às seguintes classes:
- Predicados de estado, sem quantificadores temporais nem plicas (podem incluir predicados da forma $\mathsf{ENABLED}\ A$, onde $A$ é uma action).
- Invariantes da forma $\square\ P$, onde $P$ é um predicado de estado.
- Invariantes de transição da forma $\square [A]_t$, onde $A$ é uma action e $t$ uma expressão envolvendo as variáveis de estado.
- Fórmulas temporais simples, isto é, qualquer fórmula em lógica temporal linear clássica sem actions (combinação de predicados de estado usando conectivas lógicas e operadores temporais), ou combinações deste tipo de fórmulas com fórmulas do tipo $\lozenge \square [A]_t$ usando conectivas lógicas. As fórmulas do tipo $\lozenge \square [A]_t$ vão ser importantes na verificação de propriedades de liveness, como veremos na próxima aula.
Para usar o TLC é necessário começar por criar um model que define o valor de todas os parâmetros constantes. Depois teremos que selecionar qual a definição que especifica o comportamento do algoritmo (ou separadamente o predicado que define os estados iniciais e a action que define a relação de transição). Finalmente, podemos selecionar quais as propriedades que se pretende verificar.
Por omissão, o TLC verifica sempre a ausência de deadlock no algoritmo. Se Next contiver a definição da relação de transição, esta propriedade define-se como [](ENABLED(Next)). Em algoritmos concorrentes é frequente desejar-se esta propriedade, mas em alguns algoritmos (nomeadamente algoritmos que terminam) pode não fazer sentido.
Exercício: use o TLC para verificar as propriedades de safety das especificações TLA+ anteriores; verifique também que os algoritmos de exclusão mútua não têm deadlocks.
Exercício: no algoritmo de exclusão mútua de Peterson para N > 1 processos, como poderia usar o TLC para mostrar um exemplo de um traço onde todos processos conseguem entrar na região crítica?
Exercício: use o TLC para verificar que no puzzle da cadeira pesada introduzido na primeira aula, realmente não é possível colocar a cadeira na quadrícula imediatamente ao lado direito com a mesma orientação que estava inicialmente, considerando que a mesma só se pode movimentar num mapa quadriculado de dimensão 10 x 10.