MFP

Índice
| Métodos Formais em Engenharia de Software |
|---|
| Cálculo de Sistemas de Informação |
| Programação Ciber-física |
| Verificação Formal |
| Projecto em MFP |
| Anos anteriores |
| Calendário | Sumários |
| Alumni |
Verificação Formal: Aula 2
Sistemas de transição de estados
Um dos modelos mais comuns da computação são os sistemas de transição de estados. Um sistema de transição de estados inclui:
- Um conjunto de estados $S$.
- Um conjunto de estados iniciais $I \subseteq S$.
- Uma relação de transição entre estados $R \subseteq S \times S$.
Um comportamento (ou traço) do sistema é uma sequência de estados $\pi = s_0,s_1,s_2,\ldots$ tal que $s_0 \in I$ e $\forall i \in \mathbb{N} \cdot (s_i,s_{i+1}) \in R$. Para simplificar a semântica da lógica temporal que vamos usar para especificar as propriedades destes sistemas, é frequente assumir-se que todos os comportamentos possíveis são infinitos. Para tal exige-se que a relação $R$ seja total, ou seja, $\forall s \in S \cdot \exists s’ \in S \cdot R(s,s’)$.
Semântica de algoritmos imperativos
Podemos dar semântica a algoritmos imperativos usando sistemas de transição de estados. Os estados possíveis correspondem a todas as possíveis valorações das variáveis usadas no algoritmo. No entanto, para se conseguir distinguir em que ponto da execução se encontra o algoritmo é necessário incluir uma variável extra por cada processo (um program counter) que distingue qual a instrução que vai ser executada a seguir. Para facilitar a especificação vamos etiquetar as instruções do algoritmo, tal como no seguinte algoritmo para calcular o valor absoluto.
var r : integer = n;
0: if r < 0 then
1: r := -r
2:
Como o valor de n é arbitrário, para este algoritmo teremos um conjunto infinito de possíveis estados. Nem todos estes estados são acessíveis a partir de um estado inicial. Por exemplo, estados onde n = 3 e r = 10 não serão acessíveis. Ao desenhar o sistema de transição que modela um algoritmo vamos usualmente mostrar apenas os estados acessíveis a partir de estados iniciais, tal como no sistema de transição seguinte que modela o algoritmo acima. Note os lacetes nos estados terminais, por forma a cumprir o requisito de a relação de transição ser total: vamos assumir que após terminar a execução, o algoritmo fica num livelock no program counter final.
Como referido acima, no caso de algoritmos concorrentes será necessário um program counter por cada processo.
var x : integer = 0
procedure increment;
begin
0: x := x + 1
1: end;
increment || increment
Exercício: desenhe o sistema de transição de estados correspondente ao seguinte algoritmo concorrente.
var
x : integer = 0;
procedure increment;
var
y : integer = 0;
begin
0: y := x;
1: x := y + 1
2: end;
increment || increment
Exercício: desenhe o sistema de transição de estados correspondente ao seguinte algoritmo concorrente.
var x : integer = 0
procedure increment;
begin
0: x := x + 1
1: end;
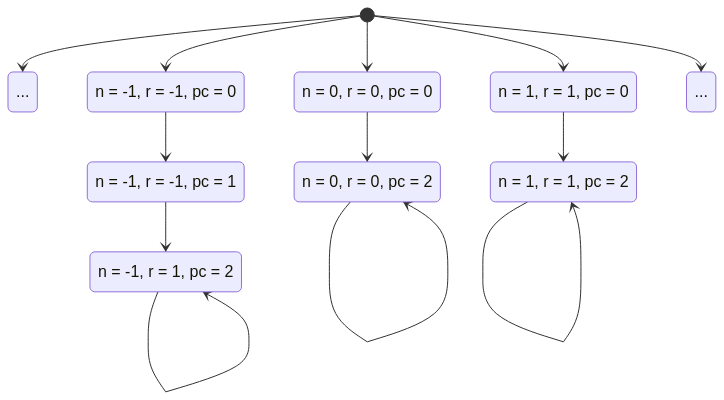
increment || increment || increment
Exercício: quantos comportamentos possíveis tem este algoritmo? se em vez de 3 tivéssemos $N$ processos quantos comportamentos possíveis haveria?
Atomicidade
Para simplificar a modelação e análise estamos a assumir que todas as instruções de um processo executam de forma atómica, isto é sem interrupção de outros processos. Por exemplo, no algoritmo com duas threads assumimos que x := x + 1 executa de forma atómica. De facto, isto não é garantido pois a execução desta instrução implica uma leitura da memória do valor actual de x e uma posterior escrita de x + 1. Entre estas duas instruções máquina o processo poderia ser interrompido, pelo que na prática a execução desta instrução é semelhante a executar as instruções y := x; x := y+1 assumindo que y é uma variável local do processo.
Por vezes, para simplificar ainda mais a modelação e tornar a análise mais eficiente (porque o número de traços possíveis diminui significativamente) vamos agrupar várias instruções para executar de forma atómica. Para sinalizar isso iremos simplesmente reduzir o número de etiquetas no algoritmo e assumir que todas as instruções entre duas etiquetas executam de forma atómica. Note que em algoritmos concorrentes isto pode mascarar potenciais problemas e tal deve ser feito com muito cuidado. Em algoritmos distribuídos é mais frequente fazer isso, e assumir, por exemplo, que todo o código que processa uma determinada mensagem recebida executa de forma atómica.
Por exemplo, em vez de 3 podemos colocar apenas 2 etiquetas no algoritmo que calcula o valor absoluto, fazendo com que todo o condicional execute de forma atómica.
var r : integer = n;
0: if r < 0 then r := -r
1:
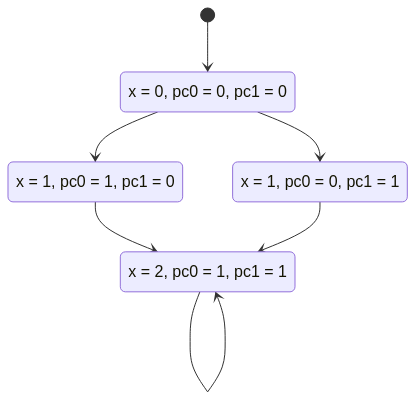
Neste caso o sistema de transição de estados que modela este algoritmo passaria a ser o seguinte.
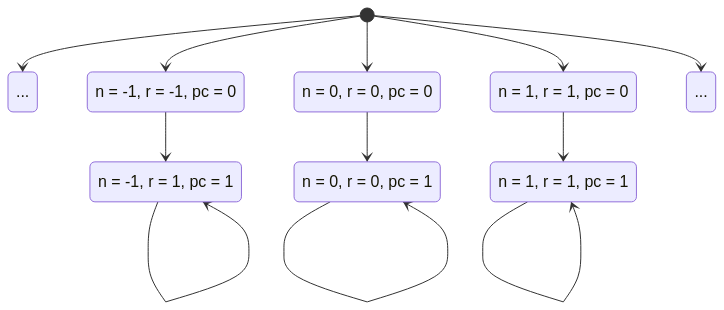
Já no exemplo com 2 processos que incrementam uma variável partilhada, mas que primeiro fazem uma cópia da mesma para uma variável local, se executarmos as 2 atribuições de forma atómica passamos a ter um sistema de transição equivalente ao que modela a versão desse algoritmo sem cópia local.
var
x : integer = 0;
procedure increment;
var
y : integer = 0;
begin
0: y := x;
x := y + 1
1: end;
increment || increment
Considere a a seguinte versão do algoritmo de Peterson, onde usamos atomicidade para dividir a execução de cada processo em três fases: pedir para entrar na região crítica (etiqueta 0); esperar para entrar (etiqueta 1); e sair da região crítica (etiqueta 2).
var
turn : 0..1;
want0 : boolean = false;
want1 : boolean = false;
procedure process0;
begin
while true do
begin
0: (* idle *)
want0 := true;
turn := 1;
1: repeat until (not want1 or turn = 0);
(* critical *)
2: want0 := false
end
end;
procedure process1;
begin
while true do
begin
0: (* idle *)
want1 := true;
turn := 0;
1: repeat until (not want0 or turn = 1);
(* critical *)
2: want1 := false
end
end;
process0 || process1
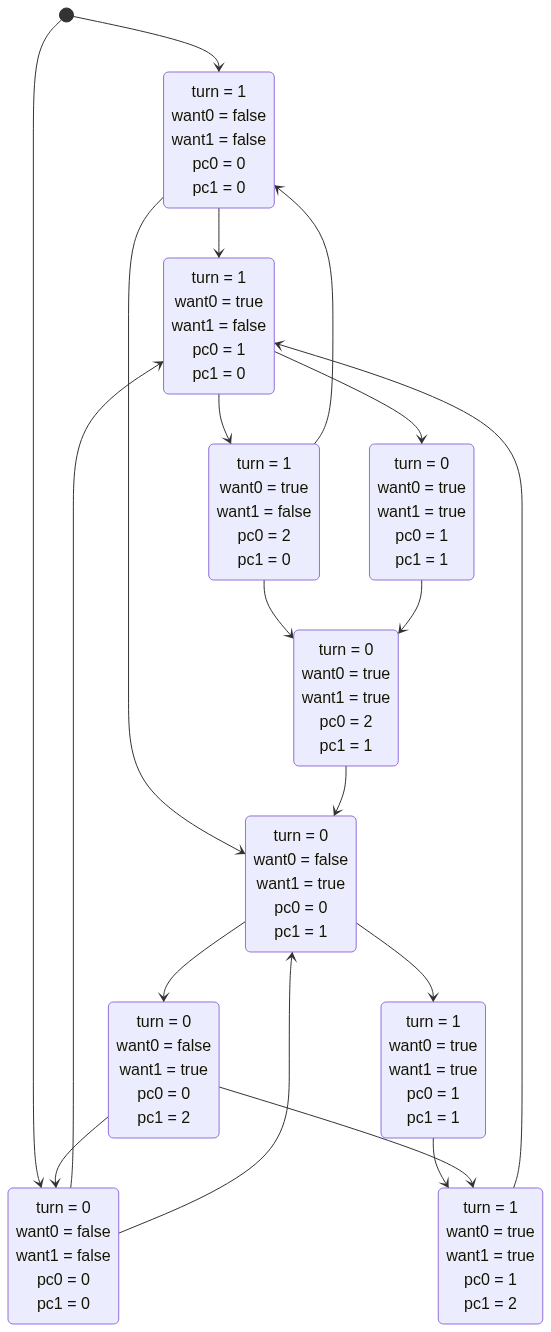
Este algoritmo seria modelado pelo seguinte sistema de transição.
Como se pode ver neste exemplo, mesmo um sistema de transição finito pode ter um número infinito de comportamentos diferentes!
Exercício: desenhe o sistema de transição correspondente ao seguinte algoritmo de exclusão mútua que usa um semáforo para controlar o acesso à região crítica.
var
sem : boolean = true;
procedure process;
begin
0: while true do
begin
(* idle *)
1: repeat until sem;
sem := false;
(* critical *)
2: sem := true;
end
end;
process || process
Lógica Temporal Linear
Para especificar propriedades de algoritmos reativos, concorrentes ou distribuídos, é frequente usar-se lógica temporal linear (Linear Temporal Logic). A ideia de especificar propriedades de algoritmos desta natureza usando lógica temporal deve-se a Amir Pnueli, ideia pela qual recebeu um prémio Turing em 1996. Ao contrário das asserções usadas na lógica de Hoare, cuja validade é verificada num estado do algoritmo, as asserções em lógica temporal linear são verificadas em comportamentos do algoritmo, ou seja, sequências de estados possíveis. Um algoritmo satisfaz uma asserção em lógica temporal sse esta for válida em todos os seus possíveis comportamentos. Para além das conectivas usuais da lógica proposicional, na versão mais simples da lógica temporal temos as conectiva temporais $\square$ (always) e $\bigcirc$ (next ou after), que, quando aplicada a uma proposição, verificam se esta é válida em todos os estados de um comportamento ou no estado seguinte, respetivamente. A gramática desta lógica é então definida como
\[\begin{array}{lcl} \mathit{formula} & \doteq & \mathit{predicate}\\ & \mid & \neg \mathit{formula}\\ & \mid & \mathit{formula} \wedge \mathit{formula}\\ & \mid & \bigcirc\ \mathit{formula}\\ & \mid & \square\ \mathit{formula} \end{array}\]onde $\mathit{predicate}$ é um predicado arbitrário envolvendo as variáveis do algoritmo.
A semântica da lógica temporal linear é definida sobre sistemas de transição de estados. Uma fórmula é válida num sistema de transição sse for válida em todos os seus comportamentos. O facto de uma fórmula $F$ ser válida num comportamento $s_0,s_1,\ldots$ é denotado por $s_0, s_1, \ldots \models F$. Esta noção de validade pode ser definida recursivamente na estrutura das fórmulas da seguinte forma ($F$ e $G$ representam fórmulas arbitrárias e $P$ um predicado arbitrário).
\[\begin{array}{lcl} s_0,s_1,\ldots \models P & \equiv & s_0 \models P\\ s_0,s_1,\ldots \models \neg F & \equiv & s_0,s_1,\ldots \not\models F \\ s_0,s_1,\ldots \models F \wedge G & \equiv & s_0,s_1,\ldots \models F \wedge s_0,s_1,\ldots \models G\\ s_0,s_1,\ldots \models \bigcirc F & \equiv & s_1,s_2,\ldots \models F\\ s_0,s_1,\ldots \models \square F & \equiv & \forall i \ge 0 \cdot s_i,s_{i+1},\ldots \models F \end{array}\]Usando estas conectivas podemos definir alguns operadores derivados, por exemplo, $F \vee G \doteq \neg (\neg F \wedge \neg G)$ ou $F \Rightarrow G \doteq \neg F \vee G$. Temos também o operador derivado $\lozenge$ (eventually), que se define como $\lozenge F \doteq \neg \square \neg F$. Também podemos definir diretamente a semântica deste operador da seguinte forma.
\[\begin{array}{lcl} s_0,s_1,\ldots \models \lozenge F & \equiv & \exists i \ge 0 \cdot s_i,s_{i+1},\ldots \models F \end{array}\]Alguns exemplos de fórmulas LTL e a respetiva semântica informal (onde $P$ e $Q$ representam predicados arbitrários):
- $P$, o predicado $P$ é verdade em todos os estados iniciais.
- $\square P$, o predicado $P$ é verdade em todos os estados de todos os comportamentos.
- $\lozenge P$, o predicado $P$ será inevitavelmente verdade nalgum estado de todos os comportamentos.
- $\square (P \Rightarrow \lozenge Q)$, sempre que $P$ é verdade $Q$ terá que inevitavelmente ser verdade depois.
- $\lozenge \square P$, em todos os comportamentos vai-se atingir um estado onde a partir do qual $P$ é sempre verdade.
- $\square \lozenge P$, o predicado $P$ é recorrentemente verdade em todos os comportamentos.
As duas propriedades fundamentais do algoritmo de exclusão mútua de Peterson podem ser expressas da seguinte forma:
- $\square \neg (pc_0 = 2 \wedge pc_1 = 2)$, os dois processos nunca estão na região critica ao mesmo tempo (mutual exclusion).
- $\square (pc_0 = 1 \Rightarrow \lozenge (pc_0 = 2)) \wedge \square (pc_1 = 1 \Rightarrow \lozenge (pc_1 = 2))$, sempre que um processo pretende aceder à região crítica irá conseguir (no starvation).
Exercício: como poderia especificar que o este algoritmo não tem um deadlock?
Relembre o seguinte algoritmo que multiplica um inteiro não negativo a por b, colocando o resultado em r:
var
r : integer = 0;
n : integer = 0;
0: while n < a do
begin
1: n := n + 1;
2: r := r + b
end
3:
Exercício: especifique as seguintes propriedades deste algoritmo.
- No estado inicial
nertêm o valor 0. - A variável
nnunca tem um valor negativo. - O algoritmo termina sempre.
- Se inicialmente
afor não negativo, no final da execução a variávelrtem o produto deaeb. - O predicado
r = n * bé um invariante do ciclo.
Considere o seguinte algoritmo.
var
r : integer = 0;
n : integer;
0: while n >= 0 do
begin
n := n - 1;
r := mod (r + 1) 2
end
1:
Exercício: especifique as seguintes propriedades deste algoritmo.
- Se inicialmente
nfor não negativo o algoritmo termina. - Se inicialmente
nfor negativo o valor derserá recorrentemente0e recorrentemente1. - Se inicialmente
nfor par então quando o algoritmo terminaré0. - Enquanto o
nfor não negativo o valor derestá sempre a oscilar entre0e1. - O algoritmo termina logo que o
nseja negativo.
Safety vs Liveness
Considere mais uma vez as duas propriedades fundamentais do algoritmo de exclusão mútua de Peterson:
- $\square \neg (pc_0 = 2 \wedge pc_1 = 2)$, os dois processos nunca estão na região critica ao mesmo tempo.
- $\square (pc_0 = 1 \Rightarrow \lozenge (pc_0 = 2)) \wedge \square (pc_1 = 1 \Rightarrow \lozenge (pc_1 = 2))$, sempre que um processo pretende aceder à região crítica irá conseguir.
Estas duas propriedades são de uma natureza bastante diferente:
- A primeira é uma propriedade de safety que proíbe certos estados “maus” de acontecerem (neste caso os estados onde ambos os processos estão na região crítica). Um contra-exemplo para esta propriedade teria um prefixo que termina num estado “mau”, não importando o que acontece depois (qualquer comportamento com o mesmo prefixo será um contra-exemplo).
- A segunda é uma propriedade de liveness que força certos estados “bons” a acontecerem em certas condições (neste caso um estado onde um dos processos está na região crítica). Um contra-exemplo para esta propriedade tem que ser um comportamento completo onde o estado “bom” nunca chega a acontecer.
Exercício: classifique todas as propriedades anteriores como sendo de safety ou liveness; para tal pense se, para encontrar os respetivos contra-exemplos, apenas basta apresentar um prefixo finito de um comportamento, ou se teremos que apresentar todo o comportamento.
Model checking explícito
O model checking é uma técnica para verificar automaticamente se uma fórmula em lógica temporal é válida num modelo de um algoritmo (um sistema de transição de estados). Para que tal seja possível, o sistema de transição de estados tem que ser finito. Um model checker tenta encontrar um contra-exemplo para a fórmula, e se não o encontrar então a fórmula é válida.
No caso das propriedades de safety basta encontrar um prefixo que leva a um estado “mau”, logo a técnica de model checking é muito simples: basta fazer uma travessia no grafo e ver se esse estado “mau” é alcançável a partir de um estado inicial. Se quisermos garantir que é mostrado o contra-exemplo mais curto possível basta usar uma travessia breadth first. Assim, a verificação de uma propriedade de safety pode ser feita em tempo linear no tamanho do sistema de transição.
Para encontrar um contra-exemplo para uma propriedade de liveness temos que encontrar um comportamento completo (infinito) onde o estado “bom” nunca acontece. Obviamente, se quisermos mostrar esse contra-exemplo ao utilizador, ele terá que ser representado de forma finita: um prefixo finito de estados seguido de um segmento finito que se repete para sempre (um traço com um ciclo). Note que nem todos os comportamentos de um sistema de transição podem ser representados de forma finita, mas um dos resultados mais importantes da lógica temporal é que se uma fórmula não é válida então terá que ter pelo menos um contra-exemplo que pode ser representado de forma finita, pelo que o model checking pode restringir a sua procura a este tipo de comportamentos. Na prática, para encontrar contra-exemplos temos que encontrar ciclos no sistema de transição onde o estado “bom” nunca acontece.
Considere, por exemplo, a propriedade de liveness $\lozenge P$. Uma forma eficiente de encontrar contra-exemplos para esta propriedade (comportamentos com um ciclo onde todos os estados satisfazem $\neg P$) consiste em usar a seguinte técnica:
- Restringir o sistema de transição apenas aos estados que satisfazem $\neg P$.
- Calcular os componentes fortemente ligados deste sistema de transição restrito.
- Usar uma única travessia para ver se algum dos componentes fortemente ligados não triviais (componentes com mais de um estado ou com apenas um estado com um lacete) é acessível a partir de um estado inicial (a travessia é feita no grafo invertido começando nos estados dentro dos componentes fortemente ligados não triviais).
- Se tal for possível então temos um contra-exemplo, pois dentro de um componente fortemente ligado não trivial conseguimos ter um ciclo infinito.
Esta técnica pode ser generalizada para verificar qualquer fórmula em lógica temporal linear e pode ser executada em tempo linear devido ao algoritmo de calculo de componentes fortemente ligados inventado por Robert Tarjan, pelo qual recebeu um prémio Turing em 1986 (entre outros algoritmos). A ideia de usar este algoritmo para fazer model checking eficiente de fórmulas em lógica temporal deve-se a Edmund Clarke, Ernerst Emerson e Joseph Sifakis, pela qual também receberam um prémio Turing em 2007.
Esta técnica de model checking designa-se de explícita, porque constrói explicitamente o sistema de transição em memória (o espaço de memória que consome é linear). Como o número de estados cresce exponencialmente com o número de variáveis usados num algoritmo, esta técnica pode não conseguir analisar certos algoritmos. Existe uma técnica alternativa, designada de model checking simbólico, onde o sistema de transição não é construído explicitamente, mas representado implicitamente através de fórmulas.
Exercício: no seguinte sistemas de transição dê exemplos de comportamentos que podem ser representados de forma finita e comportamentos que não podem ser representados de forma finita.
Exercício: como pode ser adaptada a técnica acima apresentada para encontrar contra-exemplos para a fórmula $\square (P \Rightarrow \lozenge Q)$?
Exercício: use essa adaptação para verificar se a propriedade de no starvation é válida para algoritmos de exclusão mútua de Peterson e com semáforos.