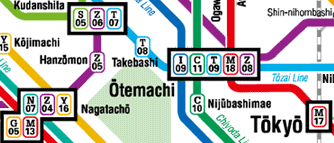
Q2.1 - Pretende-se especificar o metro de Tóquio onde (cf. figura) há várias linhas ($L$) representadas com cores diferentes, cujas paragens ($P$) estão numeradas sequencialmente e onde as estações ($E$) podem incluir paragens de linhas diferentes $-\!-$ e.g. a estação $\mathsf{Otemachi}$, que tem as paragens $\fbox{$\frac C {11}$}$, $\fbox{$\frac M {18}$}$, etc $-\!-$ permitindo aos viajantes mudar de linha.
Sabendo-se que cada paragem está sempre associada a uma e uma só estação, definiu-se o modelo simplificado
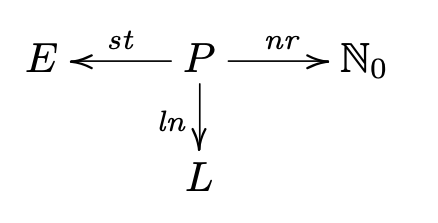
que a cada paragem associa a respectiva linha, número e estação. Por exemplo, sendo $p$ a paragem $\fbox{$\frac M {18}$}$ da figura, ter-se-á
$\begin{array}{l}st\ p = Otemachi\\\mathit{ln}\ p = M\\nr\ p = 18\end{array}$.
Claramente, o sistema de numeração das paragens das linhas necessita do seguinte invariante:
Se $n+1$ é o número de uma paragem de uma dada linha, então há outra paragem da mesma linha com o número $n$.
Qual das seguintes formulações desse invariante escolheria,
\begin{eqnarray} && \frac{nr}{succ \cdot nr} \subseteq \frac{ln}{ln} \label{eq:181128a} \\&& \nonumber\\&& \frac{nr}{succ} \subseteq nr \cdot \frac{ln}{ln} \end{eqnarray}onde $succ\ n = n+1$ é a função sucessor em $\Nat$?
Converta cada "quadrado mágico" na expressão lógica equivalente e decida, justificando.
$\Box$