CSI/2324 - Folha de exercícios práticos nrº 3

➡️ Aula de 02-Mai-2024

$ % 17-Mar-2024 \def\start{&&} \def\more{\\&&} \def\sse#1#2{{#1}\subseteq{#2}} \def\iso{\cong} \newenvironment{lcbr}{\left\{\begin{array}{l}}{\end{array}\right.} \def\ana#1{(\hskip -1ex[#1]\hskip -1ex )} \def\cata#1{(\hskip -1.1pt[\hskip 0.1pt #1 \hskip 0.1pt]\hskip -1.1pt)} \def\Seq#1{{#1}^{\star}} \def\fB{\fun B} \def\mcond#1#2#3{#1 \rightarrow #2\;,\;#3} \newenvironment{lcbr}{\left\{\begin{array}{l}}{\end{array}\right.} \def\bang{{!}} \def\Nat{\mathbb{N}} \def\N{\Nat} \def\atmost{\subseteq} \def\alt#1#2{[#1,#2]} \def\comp{\mathbin\cdot} \def\conj#1#2{\mathopen{\langle} #1, #2\mathclose{\rangle}} \def\conv#1{#1^\circ} \def\crflx#1{\Phi_{#1}} \def\dom#1{\delta {#1}} \def\from{\leftarrow} \def\fun#1{\mathsf{#1}} \def\i#1{\mathit{i}_{#1}} \def\inT{\mathsf{in}} \def\outT{\mathsf{out}} \def\implied{\Leftarrow} \def\implies{\Rightarrow} \def\just#1#2{\\&#1& \mathopen{\{}~\mbox{#2}~\mathclose{\}}\\&&} \def\ker#1{\mathbf{ker}\ {#1}} \def\img#1{\mathbf{img}\ {#1}} \def\kons#1{\underline{#1}} \def\larrow#1#2#3{#3\ \xleftarrow{#2}\ #1} \def\ldiv{\mathbin{/}} \def\p#1{\pi_{#1}} \def\plus{\mathbin{\dagger}} \def\rarrow#1#2#3{#1\ \xrightarrow{#2}\ #3} \def\rcb#1#2#3#4{\mathopen{\langle}#1 #2 : #3 : #4\mathclose{\rangle}} \def\rdiv{\mathbin{\setminus}} \def\sep{\rule{15em}{0.3pt}} \def\shrunkby{\mathbin{\upharpoonright}} \def\syd#1#2{\frac{#1}{#2}} \def\to{\rightarrow} \def\trans#1{\overline{#1}} \def\scata#1{⦅\, #1 \,⦆} \def\sep{\rule{15em}{0.3pt}} $

Q3.1 - A figura é retirada da página da Wikipedia sobre o protocolo de troca de chaves de Diffie–Hellman, onde informação numérica é simplificada sobre a forma de cores,

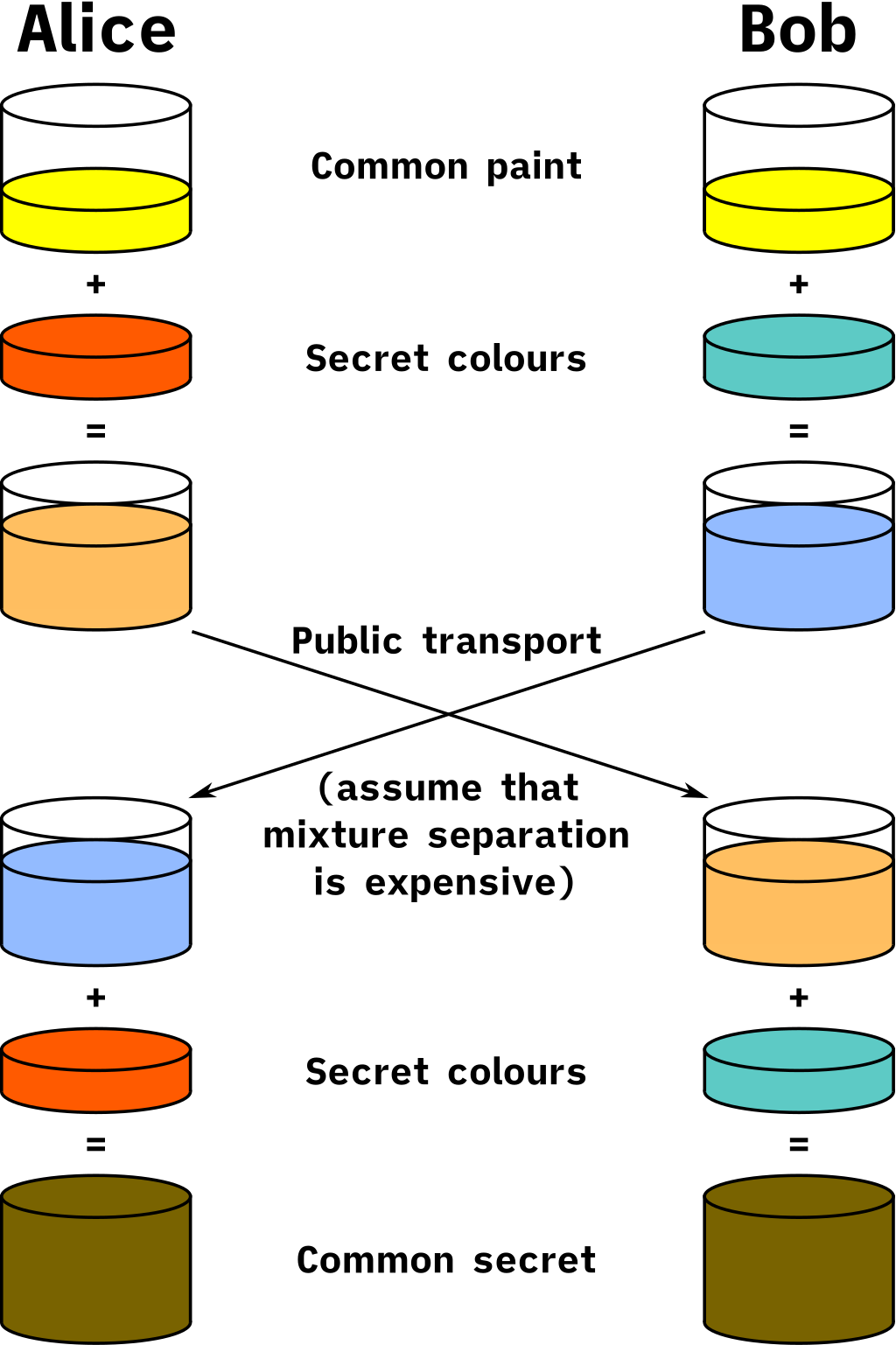
cf. também o quadro seguinte:

Passo Informaçao pública Informação privada (Alice) Informação privada (Bob)
início yellow red cyan
1 orange = yellow + red blue = yellow + cyan
2 orange, blue
fim brown = blue + red brown = orange + cyan

O protocolo assume que $f = (yellow +)$ tem uma inversa à esquerda $g$ (i.e. tal que $g \cdot f = id$), e que $g$ é computacionalmente muito complexa.

Contudo, para o "common secret" poder ser obtido de forma independente por Alicee Bob é preciso que um "quadrado mágico"

\begin{eqnarray} R\ \cdot S \subseteq P \cdot Q \end{eqnarray}

se verifique para uma determinada escolha de $R$, $S$, $P$ e $Q$. Identifique essa escolha e justifique-a.

$\Box$

Q3.2 - Uma tabela de hashing $HT$ é uma relação que satisfaz a propriedade

\begin{eqnarray} HT \subseteq \frac{id}{hash} \end{eqnarray}

onde $ hash : A \rightarrow Int$ é uma função de hashing pré-definida.

  1. Qual é o tipo de $HT$?
  2. E o que pode dizer sobre o significado de $\ a\ HT\ k\ $?
  3. Se a função $hash$ for injectiva (como em teoria pelo menos deveria ser) o que pode dizer quanto a $HT$?

$\Box$

Q3.3 - Terminado um teste de uma dada disciplina, dividem-se os testes por dois docentes que os corrigem em paralelo. No final, cada um regista as notas numa relação de tipo $Nr \rightarrow Nota$, onde consta o número de cada aluno e a respetiva nota.

No momento de se juntarem essas duas relações numa só, para se publicarem as notas, surge a dúvida: e se tiver havido enganos na leitura dos números que os estudantes escreveram nos testes?

Como critério de verificação apareceram duas sugestões:

  1. nenhum número de aluno pode aparecer em ambas as relações
  2. se um número aparecer repetido nas duas relações, a nota respectiva é a mesma.

Supondo então essas duas relações, $\def\Nota{\mathit{Nota}}$

como especificação da propriedade 1) escreveu-se:

\begin{eqnarray} R\ \cdot S \subseteq \bot \end{eqnarray}

a) Concorda com essa especificação? Justifique, corrigindo-a se necessário.

b) Especifique o critério 2.

c) Codifique este problema e os seus dois critérios em Alloy e valide-o no Alloy Analyser.

$\Box$

Q3.4 - Na questão anterior pode haver um problema adicional:

Aparecerem nos testes números de alunos que não estão inscritos na disciplina.

Constando os alunos inscritos de uma outra relação $I : Nr \rightarrow Nome$, especifique relacionalmente o critério de verificação necessário.

$\Box$