$ % 01-Mar-2024 \def\iso{\cong} \newenvironment{lcbr}{\left\{\begin{array}{l}}{\end{array}\right.} \def\ana#1{(\hskip -1ex[#1]\hskip -1ex )} \def\cata#1{(\hskip -1.1pt[\hskip 0.1pt #1 \hskip 0.1pt]\hskip -1.1pt)} \def\Seq#1{{#1}^{\star}} \def\fB{\fun B} \def\mcond#1#2#3{#1 \rightarrow #2\;,\;#3} \newenvironment{lcbr}{\left\{\begin{array}{l}}{\end{array}\right.} \def\bang{{!}} \def\Nat{\mathbb{N}} \def\N{\Nat} \def\atmost{\subseteq} \def\alt#1#2{[#1,#2]} \def\comp{\mathbin\cdot} \def\conj#1#2{\mathopen{\langle} #1, #2\mathclose{\rangle}} \def\conv#1{#1^\circ} \def\crflx#1{\Phi_{#1}} \def\dom#1{\delta {#1}} \def\from{\leftarrow} \def\fun#1{\mathsf{#1}} \def\i#1{\mathit{i}_{#1}} \def\implied{\Leftarrow} \def\implies{\Rightarrow} \def\just#1#2{\\& \mathopen{\{}~\mbox{#2}~\mathclose{\}}\\&&} \def\kons#1{\underline{#1}} \def\larrow#1#2#3{#3\ \xleftarrow{#2}\ #1} \def\ldiv{\mathbin{/}} \def\p#1{\pi_{#1}} \def\plus{\mathbin{\dagger}} \def\rarrow#1#2#3{#1\ \xrightarrow{#2}\ #3} \def\rcb#1#2#3#4{\mathopen{\langle}#1 #2 : #3 : #4\mathclose{\rangle}} \def\rdiv{\mathbin{\setminus}} \def\sep{\rule{15em}{0.3pt}} \def\shrunkby{\mathbin{\upharpoonright}} \def\syd#1#2{\frac{#1}{#2}} \def\to{\rightarrow} \def\trans#1{\overline{#1}} \def\scata#1{⦅\, #1 \,⦆} \def\sep{\rule{15em}{0.3pt}} $
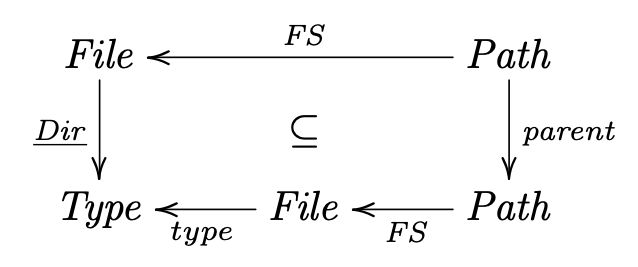
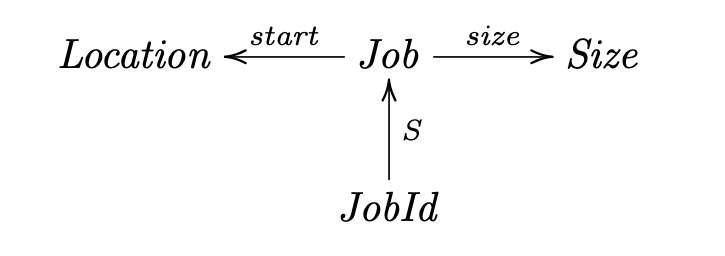
Q1.1 - Considere a relação $\larrow {Ocean} R {Continent}$ que se segue
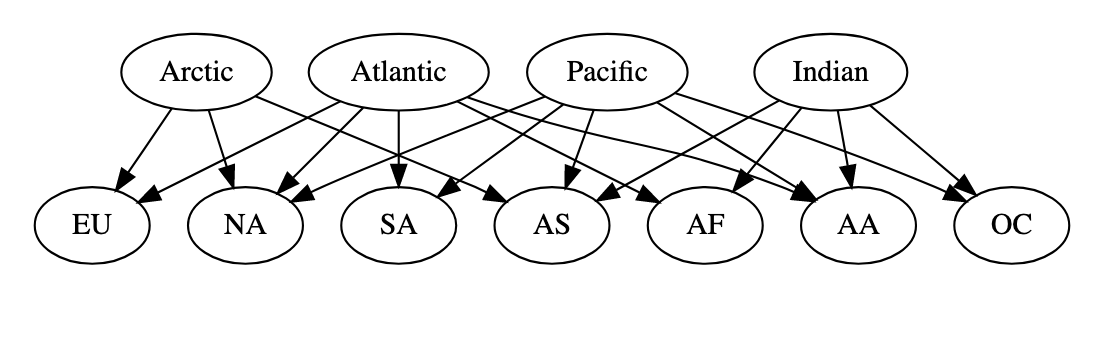
em que $y\ R\ x$ quer dizer:
O continente $y$ é banhado pelo oceano $x$
e onde as siglas abreviam continentes (e.g. $NA$ = North America, $AF$ = Africa, etc.)
Classifique a relação $R$ quanto a ser: (a) inteira; (b) reflexiva; (c) sobrejectiva; (d) simples; (e) injectiva. Justifique a sua resposta.
$\Box$
Q1.2 - Caracterizar as relações do diagrama
$\Box$
Q1.3 - Uma linha de caminho de ferro é feita de dois carris paralelos onde, a uma determinada distância da sua origem, medida em metros ($\Nat$), podem aparecer junções ou sinais. Suponha a linha representada por duas relações:
A seguinte propriedade é desejável:
\begin{eqnarray} J \subseteq \top \comp S \comp \leq \end{eqnarray}$\Box$
Q1.4 Assuma que, num sistema de ficheiros ($\def\FS{\mathit{FS}}\FS$), cada ficheiro ($\def\File{\mathit{File}}\File$) é acedido por uma única $Path$. Atente no "quadrado mágico" que se segue,
Todo o ficheiro pertence a uma directoria, que é um ficheiro especial de tipo $Dir$.
É fácil de ver que o sistema de ficheiros vazio, $\FS = \bot$, satisfaz esse invariante. Mas, e o que dizer de um sistema apenas com um ficheiro, e.g. $\FS = \kons k \comp \conv{\kons p}$, onde $k$ é o descritor do ficheiro e $p$ a sua path?
Substitua $\FS$ por $\kons k \comp \conv{\kons p}$ no quadrado acima, simplifique e tire conclusões.
$\Box$
Q1.5 - Suponha que faz parte da equipa que está a desenvolver, com base nas relações
o módulo de gestão de memória do "kernel" de um sistema operativo, onde:
O mais importante dos invariantes deste modelo é o que vai garantir que nenhum processo executa em células de memória de outros processos. Para o especificar, definiu-se a relação \begin{eqnarray} \def\Owns{\mathit{Owns}} \Owns : \JobId \leftarrow Location \end{eqnarray} que indica a "posse" (ou não) de um endereço $a$ por parte de um processo $k$:
\begin{eqnarray} k\ \Owns\ a\ &=& \langle \exists\ x\ :\ x\ S\ k\ :\ start\ x\ \leq\ a\ \leq start\ x + size\ x \rangle \end{eqnarray}Que propriedade(s) imporia à relação $\Owns$ para garantir o invariante pretendido? Justifique convenientemente a sua resposta.
$\Box$