CSI/2223 - Folha de exercícios nr. 2

16-Mar-2023

$ \def\conv#1{#1^\circ} \def\comp{\mathbin\cdot} \def\atmost{\subseteq} \def\to{\rightarrow} \def\sep{\rule{15em}{0.3pt}} \def\rcb#1#2#3#4{\mathopen{\langle}#1 #2 : #3 : #4\mathclose{\rangle}} \def\larrow#1#2#3{#3\ \xleftarrow{#2}\ #1} \def\rarrow#1#2#3{#1\ \xrightarrow{#2}\ #3} \def\Nat{\mathbb{N}} \def\conj#1#2{\mathopen{\langle} #1, #2\mathclose{\rangle}} $

---

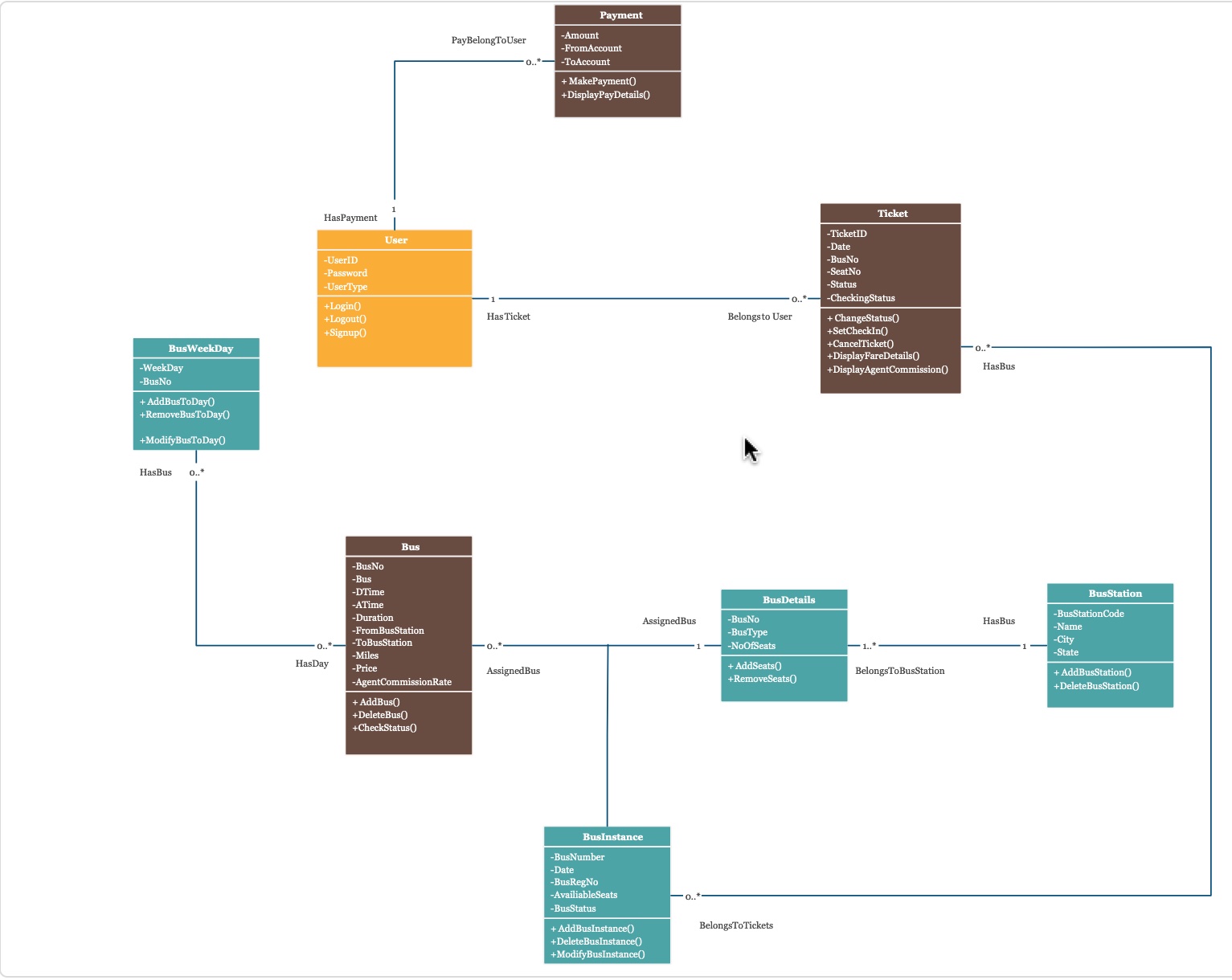
Q2.1 - Começando por analisar o diagrama relacional que descreve a Mercearia da D. Acácia,

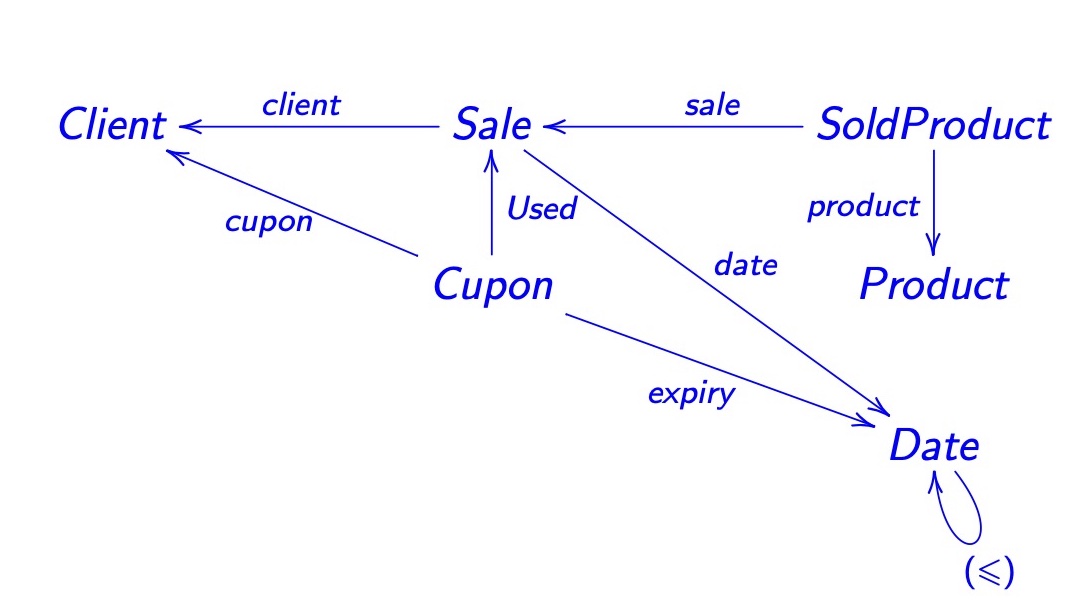
1. Que tipo de relação deverá ser $\mathit{Used}\ $?

2. Escreva sob a forma de um "quadrado mágico", $R\ \cdot S \subseteq P \cdot Q$, cada um dos invariantes:

   • Não se podem aceitar nas vendas cupões de desconto fora da sua data de validade.
   • Os cupões de descontos só podem ser usados pelos clientes para quem foram emitidos.

$\Box$

Resolução:

1. Um cupão só pode ser usado numa compra. Logo $Used$ tem de ser simples.

2. Propõe-se:

   • $ date \comp Used \atmost (\leq) \comp expiry $
   • $ client \comp Used \atmost cupon $

---

Q2.2 - Com base nas multiciplidades da tabela

UML	Alloy	A	$ \stackrel R \rightarrow $	B
$0..*$	set	-		-
$1..*$	some	surjective		entire
$0..1$	lone	injective		simple
$1..1$	one = lone + some	function$^\circ$		function

apura-se, por exemplo

$User\ {}^{\underleftarrow{has\_payment}}\ Payment $ (i.é, uma função)

ao analisar o diagrama UML abaixo (créditos: creately.com) de um On-line bus reservation system.

De facto, até se podia renomear essa função para: $User\ {}^{\underleftarrow{is\_the\_user\_who\_paid}}\ Payment $.

Caracterize as outras relações desse diagrama UML e represente-as num diagrama relacional.

$\Box$

Resolução:

Como em UML a multiplicidade 1 identifica funções, teremos ainda:

• $ \rarrow{Ticket}{belongs\_to\_user}{User} $
• $ \rarrow{BusDetails}{belongs\_to\_bus\_station}{BusStation} $ (sobrejectiva)
• $ \rarrow{Bus \times BusInstance}{assigned\_bus}{BusDetails} $

---

Q2.3 - Uma tabela de hashing $HT$ é uma relação que satisfaz a propriedade

\begin{eqnarray} HT \subseteq \frac{id}{hash} \end{eqnarray}

onde $ hash : A \rightarrow Int$ é uma função de hashing pré-definida.

• Qual é o tipo de $HT$?
• E o que pode dizer sobre o significado de $\ a\ HT\ k\ $?

$\Box$

Resolução:

• Usando a definição de divisão de funções obtém-se $HT \atmost \conv{hash}$. Logo $HT$ tem o tipo de $\conv{hash}$, isto é, $Int \to A$.

• Basta converter $HT \atmost \conv{hash}$ para lógica quantificada:

  • $\rcb\forall {a,k} {a\ HT\ k}{k = hash\ a}$

---