csi2223f01

CSI/2223 - Folha de exercícios nr. 1¶

09-Mar-2023¶

$ \def\conv#1{#1^\circ} \def\comp{\mathbin\cdot} \def\atmost{\subseteq} \def\to{\rightarrow} \def\sep{\rule{15em}{0.3pt}} \def\rcb#1#2#3#4{\mathopen{\langle}#1 #2 : #3 : #4\mathclose{\rangle}} \def\larrow#1#2#3{#3\ \xleftarrow{#2}\ #1} \def\rarrow#1#2#3{#1\ \xrightarrow{#2}\ #3} \def\Nat{\mathbb{N}} \def\conj#1#2{\mathopen{\langle} #1, #2\mathclose{\rangle}} $

Q1.1 - Caracterizar as relações do diagrama

$\Box$

Resolução:

Representar cada relação por uma matriz de $0$ e $1$, como se viu nas aulas, e classificá-la de acordo com as regras de algibeira que aí se deram.

Não esquecer que, na matriz que representa uma dada a relação $ R : A \to B$, a cada habitante de $A$ (resp. $B$) corresponde uma coluna (resp. linha).

Q1.2 - Um sistema de ficheiros $FS$ "tipo Posix":

É uma relação simples entre $Paths$ e os ficheiros propriamente ditos.
Sempre que uma aplicação acede a um ficheiro, é criado um $Descriptor$ que regista esse acesso.
Faz parte de cada $Descriptor$ a indicação da $path$ do ficheiro respectivo.
Todos os acessos a ficheiros estão registados numa relação $FT$ (file table) a que se acede a partir de um $Handle$.

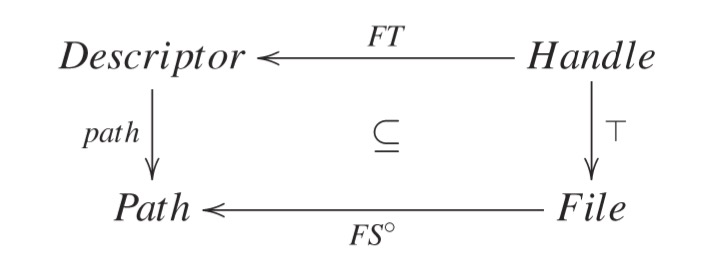
Interprete o significado da seguinte propriedade desejável (invariante), expressa relacionalmente:

\begin{eqnarray} path\ \cdot FT\ \subseteq FS^\circ \cdot \top \end{eqnarray}

Sugestão: inspecione o seu significado pointwise.

$\Box$

Resolução:

Fazendo "shunting" de $path$ obtém-se \begin{eqnarray} FT \atmost \conv{path} \comp \conv{FS} \comp\top \end{eqnarray} e daí: \begin{eqnarray} \def\rcb#1#2#3#4{\mathopen{\langle}#1\ #2 : #3 : #4\mathclose{\rangle}} \def\conj#1#2{\mathopen{\langle} #1, #2\mathclose{\rangle}} \def\conv#1{#1^\circ} \def\comp{\mathbin\cdot} \def\atmost{\subseteq} %---------------------------------- \rcb\forall{d,h}{d\ FT\ h}{\rcb\exists x {} {x\ FS\ (path\ d)}} \end{eqnarray}

Ou seja:

Só podem ser usados por $FT$ ficheiros cuja $path$ exista no file system $FS$.

Q1.3 - Para o problema anterior, formulado exactamente como aí consta, o chatGPT deu o seguinte modelo Alloy:

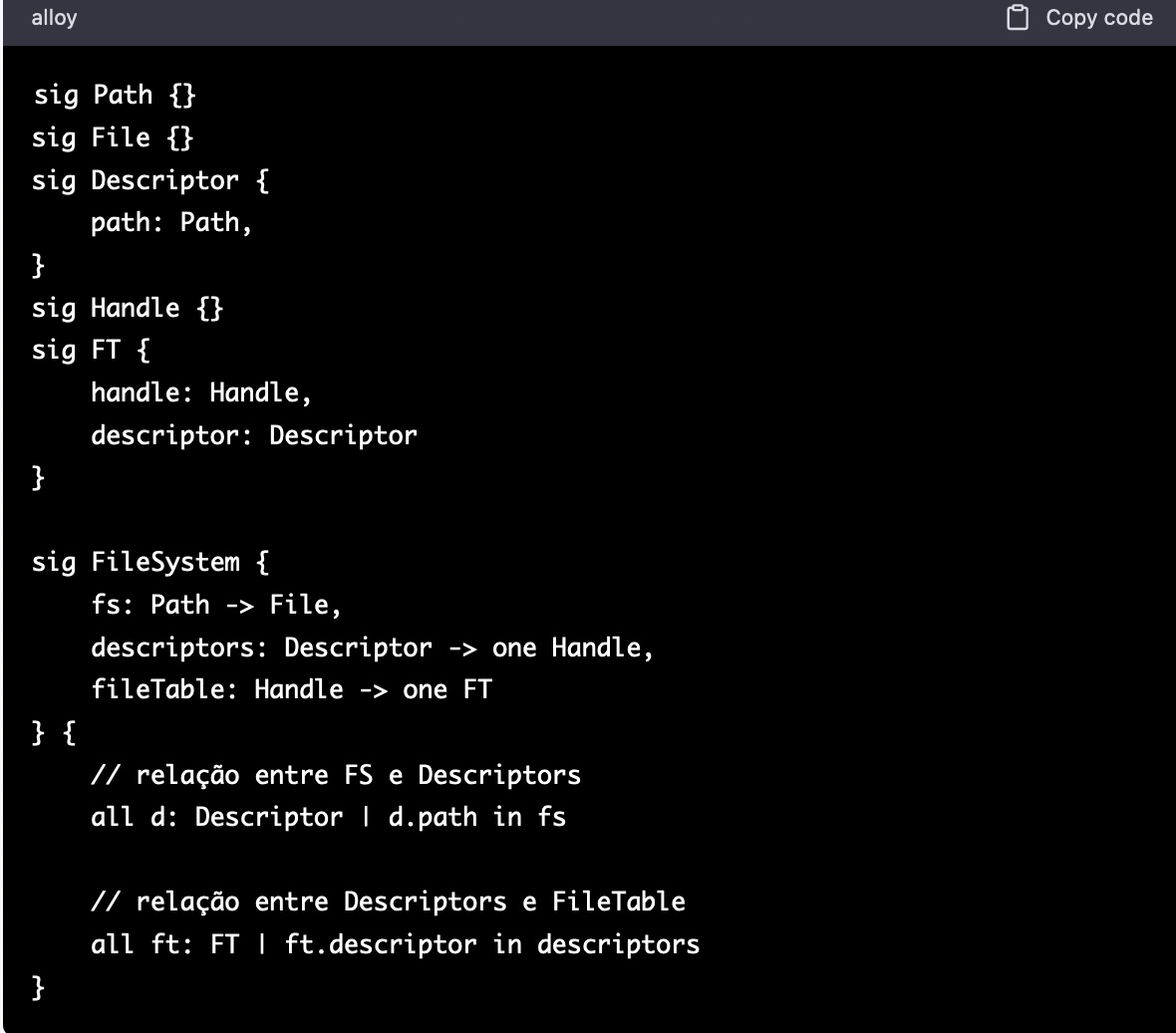
Avalie a sua qualidade em face do modelo relacional que foi dado.

$\Box$

Resolução:

Alguns defeitos (identificar mais):

FT a designar pares revela alguma confusão de conceitos
descriptors deveria ser dado onde Descriptor é defindo
fileTable repete Handle, que já está em FT
...

Q1.4 - Suponha que faz parte da equipa que está a desenvolver, com base nas relações

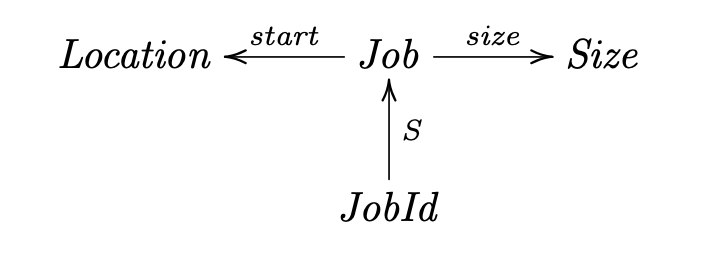
o módulo de gestão de memória do ``kernel" de um sistema operativo, onde:

$JobId$ identifica cada processo ($Job$) em execução, de forma única;
$start$ dá o endereço onde começa o bloco de memória reservado a cada processo em execução;
$size$ dá o tamanho desse bloco de memória (contígua);
$S$(cheduled) é a relação simples que associa $JobId$s a $Job$s;
$Location$ e $Size$ são números naturais.

O mais importante dos invariantes deste modelo é o que vai garantir que nenhum processo executa em células de memória de outros processos. Para o especificar, definiu-se a relação $Owns : JobId \leftarrow Location$ que indica a "posse" (ou não) de um endereço $a$ por parte de um processo $k$:

\begin{eqnarray} k\ Owns\ a\ &=& \langle \exists\ x\ :\ x\ S\ k\ :\ start\ x\ \leq\ a\ \leq start\ x + size\ x \rangle \end{eqnarray}

A que propriedade(s) da relação $Owns$ recorreria para especificar o invariante pretendido? Justifique convenientemente a sua resposta.

$\Box$

Resolução:

Claramente:

O "kernel" só deve dar o acesso a um dado endereço de memória $a$ a um só processo $k$.

Logo $Owns$ tem de ser injectiva.

Q1.5 - Terminado o teste de uma dada disciplina, dividem-se os testes por dois docentes que os corrigem em paralelo. No final, cada um regista as notas numa relação de tipo $Nr \rightarrow Nota$, onde consta o número de cada aluno e a respetiva nota.

No momento de se juntarem essas duas relações numa só, para se publicarem as notas, surge a dúvida: e se tiver havido enganos na leitura dos números que os estudantes escreveram nos testes?

Como critério de verificação apareceram duas sugestões:

nenhum número de aluno pode aparecer em ambas as relações

se um número aparecer repetido nas duas relações, a nota respectiva é a mesma.

Supondo então essas duas relações,

$R : Nr \rightarrow Nota$
$S : Nr \rightarrow Nota$

como especificação da propriedade 1) escreveu-se:

\begin{eqnarray} R\ \cdot S \subseteq \bot \end{eqnarray}

a) Concorda com essa especificação? Justifique, corrigindo-a se necessário.

b) Especifique o critério 2.

c) Codifique este problema e os seus dois critérios em Alloy e valide-o no Alloy Analyser.

$\Box$

Resolução:

a) A expressão não tipa, pois a saída de $S$ não é a entrada de $R$. Logo, uma das relações tem de ser invertida, por exemplo:

\begin{eqnarray} \def\conv#1{#1^\circ} \def\comp{\mathbin\cdot} \def\atmost{\subseteq} \conv R \comp S \subseteq \bot \end{eqnarray}

b) Propõe-se:

$ R \cup S$ é simples.

$ \def\conv#1{#1^\circ} \def\comp{\mathbin\cdot} \def\atmost{\subseteq} \def\to{\rightarrow} \def\sep{\rule{15em}{0.3pt}} $

Q1.6 - Na questão anterior pode haver um problema adicional:

Aparecerem nos testes números de alunos que não estão inscritos na disciplina.

Constando os alunos inscritos de uma outra relação $I : Nr \rightarrow Nome$, especifique relacionalmente o critério de verificação necessário.

$\Box$

Resolução:

Queremos garantir:

Se um aluno veio ao teste ($R \cup S$), então esse aluno está inscrito ($I$).

O que sugere algo como...

\begin{eqnarray} \def\conv#1{#1^\circ} \def\comp{\mathbin\cdot} \def\atmost{\subseteq} R \cup S \atmost I \end{eqnarray}

... que, contudo não tipa! Mas isso resolve-se acrescentando $\top$ ao lado superior, que "isola" os respectivos outputs:

\begin{eqnarray} \def\conv#1{#1^\circ} \def\comp{\mathbin\cdot} \def\atmost{\subseteq} R \cup S \atmost \top \comp I \end{eqnarray}

Q1.7 - Uma linha de caminho de ferro é feita de dois carris paralelos onde, a uma determinada distância da sua origem, medida em metros, podem aparecer junções ou sinais. Suponha a linha representada por duas relações:

$\def\Nat{\mathbb N } J : Junction \leftarrow \Nat$
$\def\Nat{\mathbb{N}} S : Signal \leftarrow \Nat$

Diga como especificaria relacionalmente, isto é sob a forma de um "rectângulo mágico"

\begin{eqnarray} R\ \cdot S \subseteq P \cdot Q \end{eqnarray}

a seguinte propriedade desejável num qualquer sistema ferroviário:

Antes de uma junção de via tem de haver sempre um sinal que a avise.

$\Box$

Resolução:

O que o enunciado diz, por outras palavras, é

"...se houver uma junção então ... haverá um sinal...".

que sugere $J \atmost S$ como primeira aproximação (grosseira). Contudo, $ \def\conv#1{#1^\circ} \def\comp{\mathbin\cdot} \def\atmost{\subseteq} J \atmost S $

não tipa (!)
esquece-se de que o sinal tem de vir antes da junção, cf. $(\leq)$ em $\Nat$.

Ora, isso resolve-se acrescentando $(\leq)$ para garantir o "antes" e $\top$ para isolar os outputs, o que dá:

\begin{eqnarray} J \atmost \top \comp S \comp (\leq) \end{eqnarray}

Q1.8 - Sempre que uma pessoa chega a uma Loja do Cidadão e tira um talão nas máquinas de gestão de filas, esse talão tem:

um número
um "time stamp"
a indicação da loja ou serviço pretendido.

Todos os talões são geridos num único sistema, centralizado. Como especificaria relacionalmente a informação guardada nesse sistema?

$\Box$

Resolução:

Como há uma só máquina de talões por cada loja (ou serviço) não é possível tirar o mesmo número ao mesmo tempo. Daí

\begin{eqnarray} (Loja + Serviço) \times \Nat \xrightarrow{LC} TimeStamp \end{eqnarray}

deverá ser simples e injectiva.

Q1.9 - Considere a seguinte descrição do conhecido protocolo ABP (Alternating bit protocol) tal como é descrito informalmente na Wikipedia:

Messages are sent from transmitter A to receiver B. Assume that the channel from A to B is initialized and that there are no messages in transit. Each message from A to B contains a data part and a one-bit sequence number, i.e., a value that is 0 or 1. B has two acknowledge codes that it can send to A: ACK0 and ACK1.

When A sends a message, it resends it continuously, with the same sequence number, until it receives an acknowledgment from B that contains the same sequence number. When that happens, A complements (flips) the sequence number and starts transmitting the next message.

When B receives a message that is not corrupted and has sequence number 0, it starts sending ACK0 and keeps doing so until it receives a valid message with number 1. Then it starts sending ACK1, etc.

This means that A may still receive ACK0 when it is already transmitting messages with sequence number 1. (And vice versa.) It treats such messages as negative-acknowledge codes (NAKs). The simplest behaviour is to ignore them all and continue transmitting.

The protocol may be initialized by sending bogus messages and acks with sequence number 1. The first message with sequence number 0 is a real message.

Suponha que tem acesso aos logs de um sistema de comunicação por ABP:

$Log : Time \to Message$
$origin: Message \to \{ A , \ B \}$
$bit : Message \to \{ 0 , \ 1 \}$
$data : Message \to Data$

Escreva, (para já) por palavras suas apenas, propriedades que se tenham de verificar para que um dado log registe uma sessão de comunicação bem sucedida.

$\Box$

Resolução:

A não pode mudar o seu bit de controlo enquanto não receber confirmação desse bit por B.

Por exemplo, um log que contenha pares $(origin,bit)$ como em

$…, (A,1),(A,0)…$

$…, (A,0),(B,1),(A,1)…$

corresponde a uma comunicação irregular, pois não há garantia que $B$ tenha recebido a primeira mensagem.